A convex lens of focal length 15 cm and a concave mirror of focal length 30 cm are kept with their optic axis PQ and RS parallel but separated in vertical directiion by 0.6 cm as shown . The distance between the lens and mirror is 30 cm . An upright object AB of height 1.2 cm is placed on the optic axis PQ of the lens at a distance of 20 cm from the lens . if A'B' is the image after refraction from the lens and the reflectiion from the mirror , find the distance of A'B' from the pole of the mirror and obtain its magnification . Also locate positions of A' and B' with respect to the optic axis RS.
_E01_247_Q01.png)
The correct Answer is:15 cm ,32
(a) Rays coming from object AB first refract from the lens and then reflect from the mirror .
Refraction from the lens :
u=−20cm,f=+15cm
Using lens formula 1v−1u=1f,1v−1−20=115
∴v=+60 cm and linear magnification ,
m1=vu=+60−20=−3 i.e, , first image formed by the lens will be 60 cm from it (or 30 cm from mirror) towards left and 3 times magnified but inverted
Length of first image A1,B1 would be 1.2×3=3.6 cm (inverted).
_E01_247_S01.png)
Reflection from mirror : Image formed by lens (A1,B1) will behave like a virtual object for mirror at a distance of 30 cm from it as shown . Therefore Using mirror formula ,
1v+1u=1for1v+130=−130∴v=−15cm
& linear magnification , m2=−vu=−15+30=+12
i.e. final image A'B' will be located at a distance of 15 cm from the mirror (towards right) and since magnification is +12 length of final image would be 3.6×12=1.8cm
∴A'B'=1.8 cm
Point B1 is 0.6 cm above the optic axis of mirror , therefore , its image B' would be (0.6)12=0.3 cm
above optic axis . Similarly , point A1 is 3 cm below the optic axis , therefore , its image A' will be 3×12=1.5 cm below the optic axis as shown below :
_E01_247_S02.png)
Total magnification of the image .
m=m1×m2=(−3)(+12)=−32
∴A'B'=(m)(AB)=(−32)(1.2)=−1.8 cm
Note that , there is no need of drawing the ray diagram if not asked in the questions .
Topper's Solved these Questions
Similar Questions
A convex lens of focal length 15 cm and a concave mirror of focal length 30 cm are kept with their optic axis PQ and RS parallel but separated in vertical directiion by 0.6 cm as shown . The distance between the lens and mirror is 30 cm . An upright object AB of height 1.2 cm is placed on the optic axis PQ of the lens at a distance of 20 cm from the lens . if A'B' is the image after refraction from the lens and the reflectiion from the mirror , find the distance of A'B' from the pole of the mirror and obtain its magnification . Also locate positions of A' and B' with respect to the optic axis RS.
_E01_247_Q01.png)
View SolutionA convex lens of focal length 15 cm and a concave mirror of focal length 30 cm are kept with their optic axis PQ and RS parallel but separated in vertical directiion by 0.6 cm as shown . The distance between the lens and mirror is 30 cm . An upright object AB of height 1.2 cm is placed on the optic axis PQ of the lens at a distance of 20 cm from the lens . if A'B' is the image after refraction from the lens and the reflectiion from the mirror , find the distance of A'B' from the pole of the mirror and obtain its magnification . Also locate positions of A' and B' with respect to the optic axis RS.
_E01_247_Q01.png)
View Solution
Knowledge Check
A convex lens of focal length 15 cm and concave mirror of focal length 30 cm are kept their optical axes PQ and RS parallel but separated in vertical direction by 0.6 m, as shown. The distance between the lens and mirror is 30 cm. An upright object AB of height 1.2 m is placed on the optic axic PQ of the lens at a distance of 20 cm from the lens.

Find the linear magnification of the first image after refraction from the lens.A+3B−3C+2D−2A convex lens of focal length 15 cm and concave mirror of focal length 30 cm are kept their optical axes PQ and RS parallel but separated in vertical direction by 0.6 m, as shown. The distance between the lens and mirror is 30 cm. An upright object AB of height 1.2 m is placed on the optic axic PQ of the lens at a distance of 20 cm from the lens.

Find the linear magnification of the second image after reflection from the mirror.A+2B−2C+12D−12A convex lens of focal length 15 cm and concave mirror of focal length 30 cm are kept their optical axes PQ and RS parallel but separated in vertical direction by 0.6 m, as shown. The distance between the lens and mirror is 30 cm. An upright object AB of height 1.2 m is placed on the optic axic PQ of the lens at a distance of 20 cm from the lens.

If A'B' is the final image formed, A' corresponding to A and B' corresponding to B, find the distance of B' below optics axis of lens.A0.3 mB0.5 mC0.6 mDNone of these
A convex lens of focal length 15 cm and a concave mirror of focal length 30 cm are kept with their optic axis PQ and RS parallel but separated in vertical directiion by 0.6 cm as shown . The distance between the lens and mirror is 30 cm . An upright object AB of height 1.2 cm is placed on the optic axis PQ of the lens at a distance of 20 cm from the lens . if A'B' is the image after refraction from the lens and the reflectiion from the mirror , find the distance of A'B' from the pole of the mirror and obtain its magnification . Also locate positions of A' and B' with respect to the optic axis RS.
_E01_247_Q01.png)
View SolutionA convex lens of focal length 15 cm and concave mirror of focal length 30 cm are kept their optical axes PQ and RS parallel but separated in vertical direction by 0.6 m, as shown. The distance between the lens and mirror is 30 cm. An upright object AB of height 1.2 m is placed on the optic axic PQ of the lens at a distance of 20 cm from the lens.

As in the lat problem, find the distance of A' below the optic axis of lens.
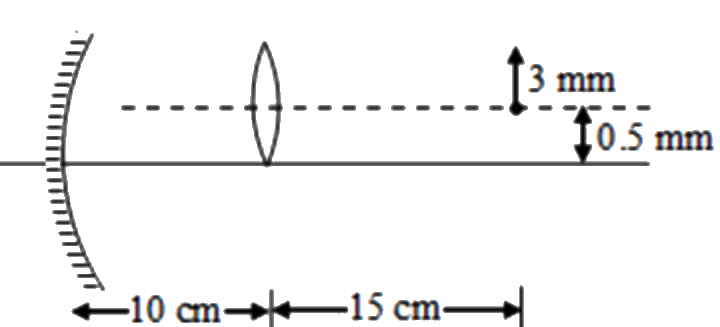
View SolutionA concave mirror of focal length 20cm and a convex lens of focal length 10(~cm) are kept with their optic axis parallel but separated by 0.5mm as shown in the figure.The distance between the lens and the mirror is 10cm. An object of height 3min is placed on the optical axis of the lens at a distance of 15∘cm from the lens. Find the height of the image (in mm ) formed by the mirror after retion from the lens.
'(##CEN_KSR_PHY_JEE_C26_E01_037_Q18##)'
View SolutionA concave mirror of focal length 20 cm and a convex lens of focal length 10 cm are kept with their optic axes parallel but separated by 0.5 mm as shown in the figure. The distance between the the lens and mirror in 10 cm. An object of height 3 mm is placed on the optic axis of lens at a distance between the lens and mirror is 10 cm. An object of height 3 mm is placed on the optic axis of lens at a distance 15 cm from the lens. Find the length of the image formed the mirror in mm.
View SolutionA convex lens of focal length 10cm and concave lens of focal length 20cm are kept 5cm apart. The focal length of the equivalent lens is
View Solution
