One end of a brass rod 2m long and having 1cm radius is maintained at 250∘C. When a steady state is reached , the rate of heat flow acrss any cross-section is 0.5cals−1. What is the temperature of the other end K=0.26cals−1cm−1.∘C−1.
To solve the problem step-by-step, we will use the formula for heat conduction through a rod, which is given by Fourier's law of heat conduction. The formula can be expressed as:
Q=k⋅A⋅(T1−T2)L
Where:
- Q is the rate of heat flow (in cal/s),
- k is the thermal conductivity (in cal/s/cm/°C),
- A is the cross-sectional area (in cm²),
- T1 and T2 are the temperatures at the two ends of the rod (in °C),
- L is the length of the rod (in cm).
Step 1: Identify the given values
- Length of the rod, L=2m=200cm
- Radius of the rod, r=1cm
- Temperature at one end, T1=250°C
- Rate of heat flow, Q=0.5cal/s
- Thermal conductivity, k=0.26cal/s/cm/°C
Step 2: Calculate the cross-sectional area A
The cross-sectional area A of the rod can be calculated using the formula for the area of a circle:
A=πr2
Substituting the radius into the equation:
A=π(1cm)2=π⋅1=3.14cm2
Step 3: Rearrange the heat conduction formula to find T2
From the heat conduction formula, we can express T1−T2:
T1−T2=Q⋅Lk⋅A
Step 4: Substitute the known values into the equation
Now we substitute the known values into the equation:
T1−T2=0.5cal/s⋅200cm0.26cal/s/cm/°C⋅3.14cm2
Calculating the denominator:
0.26⋅3.14=0.8154cal/s/°C
Now substituting back into the equation:
T1−T2=1000.8154≈122.4°C
Step 5: Solve for T2
Now we can find T2:
T2=T1−(T1−T2)=250°C−122.4°C
Calculating T2:
T2≈127.6°C
Final Answer
The temperature at the other end of the brass rod is approximately 127.6°C.
---
- Q is the rate of heat flow (in cal/s),
- k is the thermal conductivity (in cal/s/cm/°C),
- A is the cross-sectional area (in cm²),
- T1 and T2 are the temperatures at the two ends of the rod (in °C),
- L is the length of the rod (in cm).
- Length of the rod, L=2m=200cm
- Radius of the rod, r=1cm
- Temperature at one end, T1=250°C
- Rate of heat flow, Q=0.5cal/s
- Thermal conductivity, k=0.26cal/s/cm/°C
The cross-sectional area A of the rod can be calculated using the formula for the area of a circle:
From the heat conduction formula, we can express T1−T2:
Now we substitute the known values into the equation:
Now we can find T2:
The temperature at the other end of the brass rod is approximately 127.6°C.
Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - SOME WORKED OUT EXAMPLES
84 Videos
- GEOMETRICAL OPTICSBOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE -01
65 Videos
- CURRENT ELECTRICITYBOOK - ALLENCHAPTER - CURRENT ELECTRICITYEXERCISE - All Questions
427 Videos
- GRAVITATIONBOOK - ALLENCHAPTER - GRAVITATIONEXERCISE - EXERCISE 4
9 Videos
Similar Questions
A rectangular steel tank of thickness 3 cm contains water. The water in the tank is boiled by a furnace. The level of water falls at a constant rate of 1.5 cm in 15 minutes. What will be the temperature of furnace if K for steel is 0.2cals−1m−1∘C−1 ?
View SolutionWater is boiled in a rectangular steel tank of thickness 2 cm by a constant temperature furnace. Due to vaporisation, water level falls at a steady rate of 1 cm in 9 minutes. Calculate the temperature of the furnace. Given K for steel 0.2cals−1m−1.∘C−1
View Solution
Knowledge Check
The end A of rod AB of length 1 m is maintained at 80∘C and the end B at 0∘C. The temperature at a distance of 60 cm from the end A is
A16∘CB32∘CC48∘CD64∘CMetal rods X and Y of identical cross-sectional area, have lengths 60 cm and 30 cm respectively. They are made of metals of thermal conductivities λx and λy. They are well-lagged and joined end-to-end as shown in the figure-4.43. One end of X is maintained at 100∘C and the opposite end of Y is maintained at 0∘C. When steady conditions have been .reached, the temperature of the junction is found to be 25∘C.
What is the value of λxλy ?
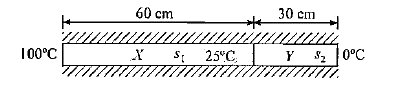 A16B23C2524D32
A16B23C2524D32The ends of the two rods of different materials with their lengths, diameters of cross-section and thermal conductivities all in the ratio 1 : 2 are maintained at the same temperature difference. The rate of flow of heat in the shorter rod is 1cals−1. What is the rate of flow of heat in the larger rod:
A1cals−1B4cals−1C8cals−1D16cals−1
Three rods of material X and three rods of material Y are connected as shown in the figure. All the rods are of identical length and cross-sectional area. If the end A is maintained at 60∘C and the junction E at 10∘C. Calculate the temperature of the junction B, C and D. The thermal conductivity of X is 0.92cal/sec−cm∘C and that of Y is 0.46cal/sec−cm−∘C.

View SolutionA bar of copper of length 75 cm and a bar of steel of length 125 cm are joined together end to end . Both are of circular cross - section with diameter 2 cm . The free ends of the copper and steel bars are maintained at 100∘C and 0∘C respectively . The surface of the bars are thermally insulted . What is the temperature of the copper - steel junction ? What is the heat transmitted per unit time across the junction ? Thermal conductivty of copper 9.2×10−2kcalm−1∘C−1s−1 and that of steel is 1.1×10−2kcalm−1s−1(∘)C−1.
View SolutionOne end of a uniform brass rod 20 cm long and 10cm2 cross-sectional area is kept at 100∘C. The other end is in perfect thermal contact with another rod of identical cross-section and length 10 cm. The free end of this rod is kept in melting ice and when the steady state has been reached, it is found that 360 g of ice melts per hour. Calculate the thermal conductivity of the rod, given that the thermal conductivity of brass is 0.25cal/scm∘CandL=80cal/g.
View SolutionCalculate the difference in temperature between two sides of an iron plate 20 m m thick, when heat is conducted at the rate of 6×105 cal/min/m2. K for metal is 0.2 cals−1cm−1.∘C−1
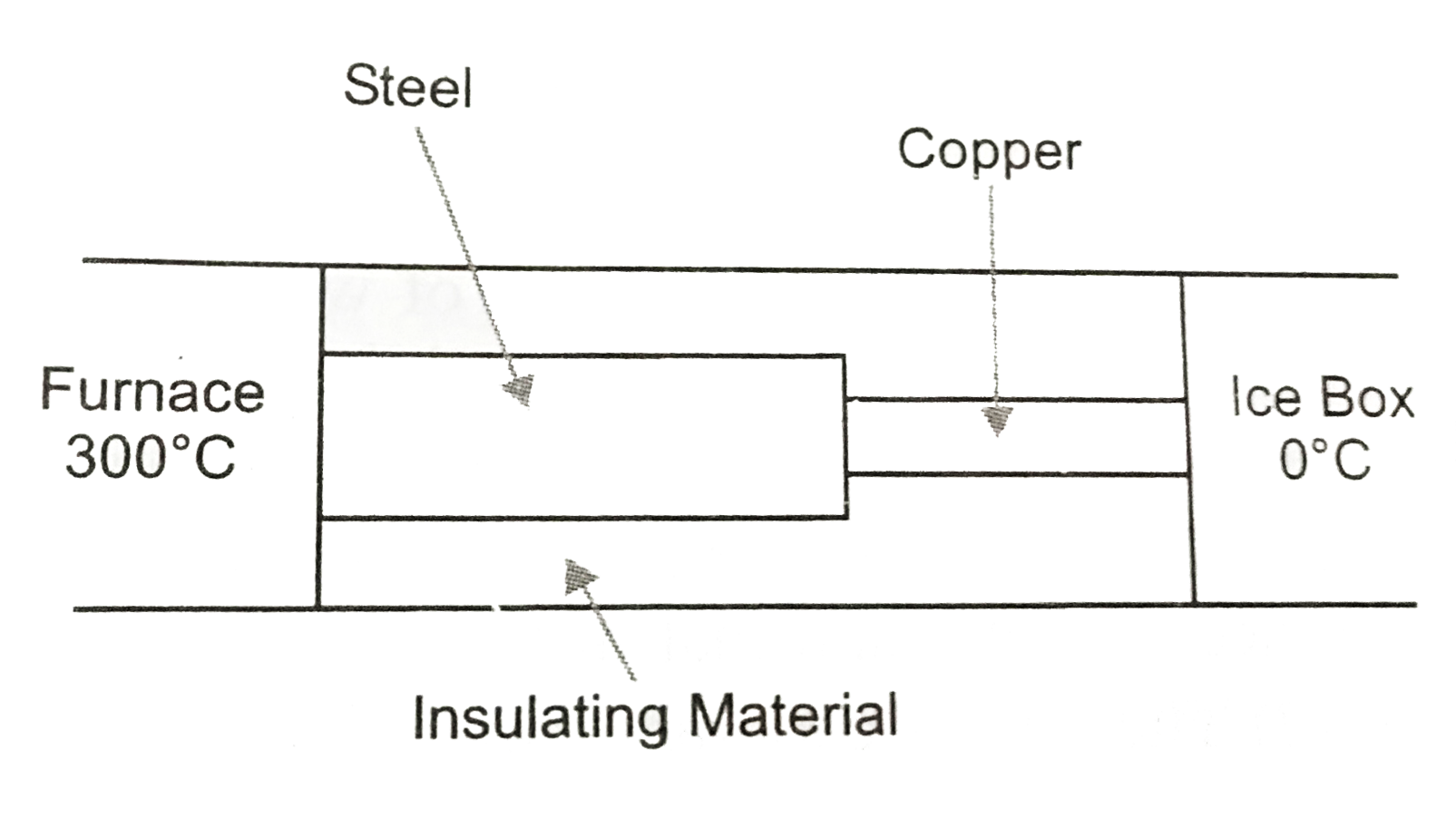
View SolutionWhat is the temperature of steel-copper jumction in the steady state of the system shown in fig. Length of the steel rod = 30.0 cm, length of the copper rod = 20.0 cm, temperature of the furnace = 300∘C, temperature of cold end =0∘C . The area of cross-section of the steel rod is twice that of the copper rod. thermal conductivity of steel = 50.2Js−1m−1.∘C−1 and of copper = 358Js−1m−1.∘C−1.
View Solution
