A bar of copper of length 75 cm and a bar of steel of length 125 cm are joined together end to end . Both are of circular cross - section with diameter 2 cm . The free ends of the copper and steel bars are maintained at 100∘C and 0∘C respectively . The surface of the bars are thermally insulted . What is the temperature of the copper - steel junction ? What is the heat transmitted per unit time across the junction ? Thermal conductivty of copper 9.2×10−2kcalm−1∘C−1s−1 and that of steel is 1.1×10−2kcalm−1s−1(∘)C−1.
To solve the problem, we need to find the temperature at the junction of the copper and steel bars and the heat transmitted per unit time across the junction.
Step 1: Identify the Given Data
- Length of copper bar, Lc=75cm=0.75m
- Length of steel bar, Ls=125cm=1.25m
- Diameter of the bars, d=2cm=0.02m
- Temperature at the free end of copper, Tc=100∘C
- Temperature at the free end of steel, Ts=0∘C
- Thermal conductivity of copper, kc=9.2×10−2kcal/m/s/∘C
- Thermal conductivity of steel, ks=1.1×10−2kcal/m/s/∘C
Step 2: Set Up the Heat Transfer Equation
Using the principle of steady-state heat transfer, we can equate the heat flow through the copper and steel sections:
kc⋅A⋅(Tc−θ)Lc=ks⋅A⋅(θ−Ts)Ls
Where:
- A is the cross-sectional area of the bars,
- θ is the temperature at the junction.
Step 3: Calculate the Cross-Sectional Area
The cross-sectional area A of the circular bars can be calculated as:
A=π(d2)2=π(0.022)2=π(0.01)2=π×10−4m2
Step 4: Substitute the Values into the Heat Transfer Equation
Substituting the values into the heat transfer equation:
9.2×10−2⋅π×10−4⋅(100−θ)0.75=1.1×10−2⋅π×10−4⋅(θ−0)1.25
Step 5: Cancel Out the Common Terms
Since A and π are common on both sides, we can cancel them out:
9.2×10−2(100−θ)0.75=1.1×10−2θ1.25
Step 6: Simplify and Solve for θ
Cross-multiplying gives:
9.2×10−2(100−θ)⋅1.25=1.1×10−2θ⋅0.75
Expanding both sides:
1.15×10−1(100−θ)=0.825×10−2θ
Distributing:
11.5−1.15θ=0.825θ
Combining like terms:
11.5=1.15θ+0.825θ
11.5=1.975θ
Now, solving for θ:
θ=11.51.975≈5.82(in degrees Celsius)
Step 7: Calculate the Heat Transmitted per Unit Time
Using the formula for heat transfer through the copper bar:
Qt=kc⋅A⋅(Tc−θ)Lc
Substituting the values:
Qt=9.2×10−2⋅π×10−4⋅(100−93.3)0.75
Calculating:
Qt=9.2×10−2⋅π×10−4⋅6.70.75
Calculating the numerical value gives:
Qt≈2.58×10−4J/s
Final Answers
- The temperature of the copper-steel junction, θ≈93.3∘C.
- The heat transmitted per unit time across the junction, Qt≈2.58×10−4J/s.
- Length of copper bar, Lc=75cm=0.75m
- Length of steel bar, Ls=125cm=1.25m
- Diameter of the bars, d=2cm=0.02m
- Temperature at the free end of copper, Tc=100∘C
- Temperature at the free end of steel, Ts=0∘C
- Thermal conductivity of copper, kc=9.2×10−2kcal/m/s/∘C
- Thermal conductivity of steel, ks=1.1×10−2kcal/m/s/∘C
Using the principle of steady-state heat transfer, we can equate the heat flow through the copper and steel sections:
- A is the cross-sectional area of the bars,
- θ is the temperature at the junction.
The cross-sectional area A of the circular bars can be calculated as:
Substituting the values into the heat transfer equation:
Since A and π are common on both sides, we can cancel them out:
Cross-multiplying gives:
Using the formula for heat transfer through the copper bar:
- The temperature of the copper-steel junction, θ≈93.3∘C.
- The heat transmitted per unit time across the junction, Qt≈2.58×10−4J/s.
Topper's Solved these Questions
- HEAT TRANSFER BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - HEAT TRANSFER EXERCISE - Illustrative Example 4.3
1 Videos
- HEAT TRANSFER BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - HEAT TRANSFER EXERCISE - Illustrative Example 4.4
1 Videos
- HEAT TRANSFER BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - HEAT TRANSFER EXERCISE - Unsolved Numerical Problems for Preparation of NSEP,INPhO&IPhO
66 Videos
- HEAT AND THERMAL EXPANSIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - HEAT AND THERMAL EXPANSIONEXERCISE - UNSOLVED NUMRICAL PROBLEMS FOR PREPARATION OF NSEP, INPhO & IPhO
82 Videos
- Kinetic Theory of Gases and Gas LawsBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - Kinetic Theory of Gases and Gas LawsEXERCISE - Unsolved Numerical Problems for Preparation of NSEP, INPhO & IPhO
64 Videos
Similar Questions
A bar of copper of length 75cm and a abr of steel of length 125cm are joined together end to end. Both are of circular cross section with diameter 2cm. The free ends of the copper and the steel bors are maintained at 100∘C and 0^(@)Crespectively.Thecurvedsurfaceofthebors.arethermally∈sa––ted.Wˆisthetemperatureofthecoppe−steeljunction?Wˆistheamountofheattransmiedperunittimeacrossthejunction?Thermalconductivityofcopperis386Js^(-1)m^(-1)^(∘)C−1 and that of steel is 46Js^(-1)m^(-1)(@)C^(-1)
View Solution+2.0 -0.0 An engineer joined a rod in which 50 cm is copper and 100 cm is steel from end to end together. Both have the circular cross-section with diameter 3 cm. If the free end of copper and steel are maintained at the temperature 100°C and 0°C respectively. Determine the temperature of the copper-steel junction. (Assume the thermal conductivity of copper and steel are 386 J/m - 5-°C. 46 J/m - 5-°C respectively) 50 cm 100 cm 100°C Copper Steel 0°C
View Solution
Knowledge Check
Cylinder copper rod of length 1m and a cylinder steel rod of length 1.5m are joined together end to end. The cross sectional area of eac rod is 3.14cm. The free ends of steel rod and copper rods are maintained at 0∘C and 100∘C respectively. The surfaces of rods are thermally insulated. Find the temperature of copper steel junction. (Given thermal conductivity of steel =46J/m−s.∘C and the thermal conductivity of copper =386J/m−s.∘C)
A40∘B60∘C93∘D80.64∘CTwo rods of similar area of cross section and length are joined as shown in the figure. The ratio of their thermal conductivity is 2:3. The free ends are maintained at 100∘C and 0∘C respectivley. THE temperature at junction in steady state is
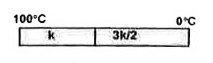 A50∘CB40∘CC60∘D80∘C
A50∘CB40∘CC60∘D80∘CA compound rod is formed of a steel core of diameter 1cm and outer casing is of copper, whose outer diameter is 2cm. The length of this compound rod is 2m and one end is maintained as 100∘C and the end is at 0∘C. If the outer surface of the rod is thermally insulated, then heat current in the rod will be (Given thermal conductivity of steel j=12cal/m/k/s, thermal conductivity of copper =92cal/m/k/s
A2cal/sB1.13cal/sC1.42cal/sD2.68cal/s
Three bars of equal lenghts and equal area of cross-section are connected in series. Their thermal conductivities are in the ratio of 2:4:3. If the open ends of the first and the last bars are at temperature 200∘C and 180∘C respectivity in the steady state, calculate the temperature of both the junctions.
View SolutionThe ends of a copper rod of length 1m and area of cross-section 1cm2 are maintained at 0∘C and 100∘C. At the centre of the rod there is a source of heat of power 25 W. Calculate the temperature gradient in the two halves of the rod in steady state. Thermal conductivity of copper is 400Wm−1K−1.
View SolutionThree bars of equal lengths x and equal area of cross-section A are connected in series. Their thermal conductivities are in the ratio 2:4:3. If the open ends of the first and the last bars are at temperatures 200∘C and 18∘C, respectively in the steady state, calculate the temperatures of both the junctions.
View SolutionThree bars of equal lengths and equal area of cross-section are connected in series fig. their thermal conducitives are in the ratio 2:3:4. If at the steady state the open ends of the first and the last bars are at temperature 200∘C and 20∘C respectively, find the temperature of both the junctions.
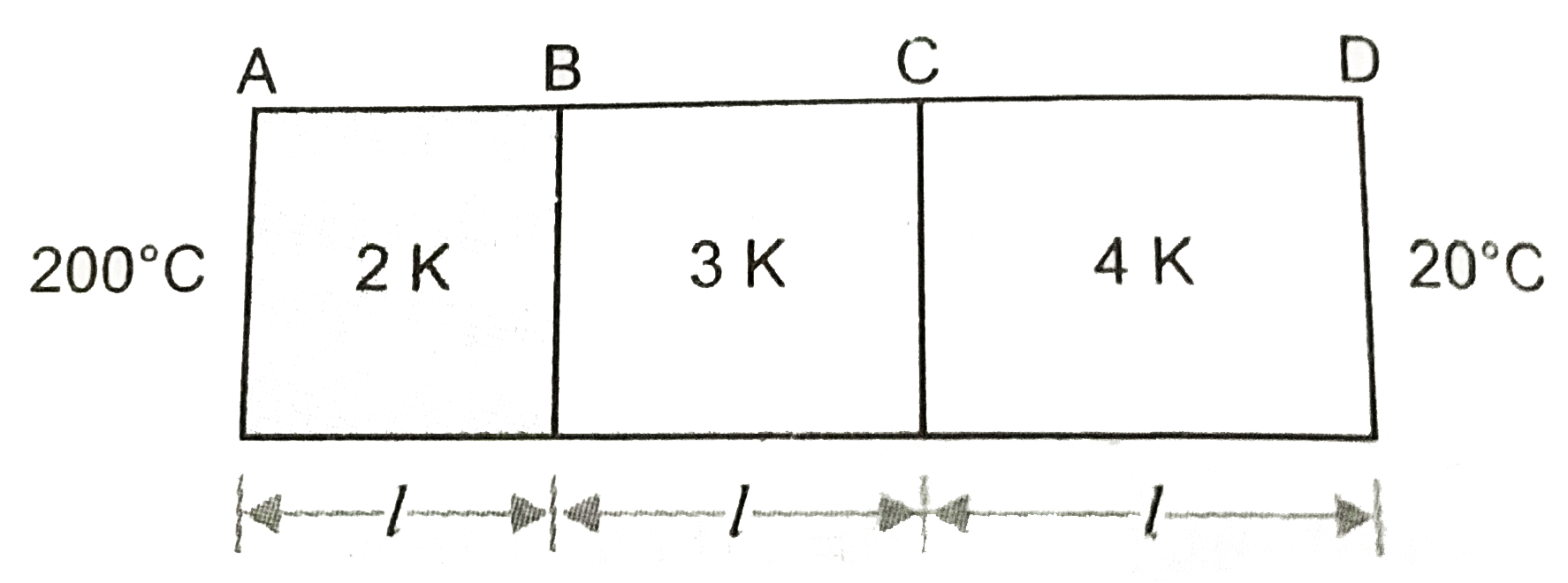 .
.
View SolutionThree metal rods made of copper, aluminium and brass, each 20cm long 4cm in diameter, are placed end to end with aluminium between the other two. The free ends of copper and brass are maintained at 100 and 0∘C respectively. Assume that the thermal conductivity of copper is twice that of aluminium and four times that of brass. The approximately equilibrium temperatures of the copper-aluminiu and aluminium-brass junctions are respectively.

View Solution
