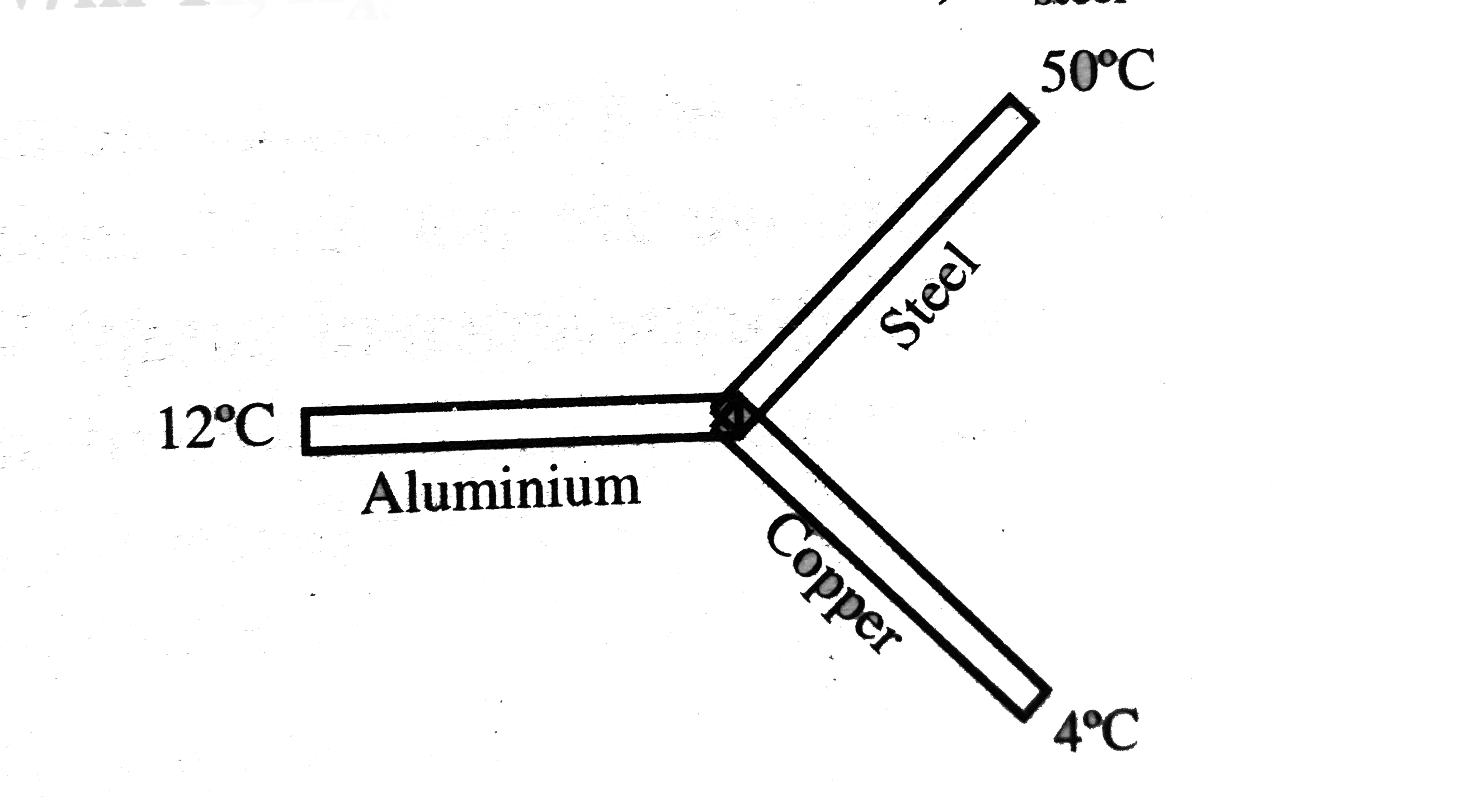
Three identical rods of length 1 m each, having cross-sectional area of 1cm2 each and made of aluminium, copper and steel, respectively, are maintained at temperatures of 12∘C,4∘C and 50∘C, respectively, at their separate ends. Find the teperature of their common junction.
[KCu=400W/m−K,KAl=200W/m−K,Ksteel=50W/m−K]
RAl=LKA=1200×10−4=104200
Similarly Rsteel=10450 and Rcopper=104400
Let temperature of common junction = T
then from Kirchoff,s current laws, iAl+isteel+iCu=0
⇒T−12RAl+T−51Rsteel+T−4RCu=0
⇒(T−12)200+(T−50)50+(T−4)400=0
⇒4(T−12)+(T−50)+8(T−4)=0
⇒13T=48+52+32=130
⇒T=10∘C
(##ALN_PHY_C07(I)_S01_010_S01.png" width="80%">
Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - SOME WORKED OUT EXAMPLES
84 Videos
- GEOMETRICAL OPTICSBOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE -01
65 Videos
- CURRENT ELECTRICITYBOOK - ALLENCHAPTER - CURRENT ELECTRICITYEXERCISE - All Questions
427 Videos
- GRAVITATIONBOOK - ALLENCHAPTER - GRAVITATIONEXERCISE - EXERCISE 4
9 Videos
Similar Questions
Three copper rods and three steel rods each of length l=10cm and area of cross-section 1cm2 are connected as shown

If ends A and E are maintained at temperatures 125∘C and 0∘C respectively, calculate the amount of heat flowing per second from the hot of cold function. [KCu=400W/m−K,Ksteel=50W/m−K]
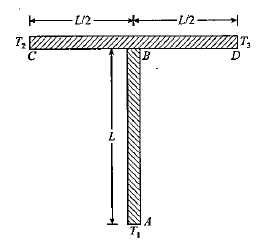
View SolutionTwo identical rods AB and CD, each of length L are connected as shown in figure-4.22. Their cross-sectional area is A and their thermal conductivity is k. Ends A, C and D are maintained at temperatures T1,T2andT3 respectively. Neglecting heat loss to the surroundings, find the temperature at B.
View Solution
Knowledge Check
Find the resistance (in mega Ω) of a wire of length 10 m, cross sectional area 1cm2 and made of a material of resistivity 100 Ωm.
A1000B20C500D10Find the resistance (in mega Ω) of a wire of length 8 m, cross sectional area 2 cm2 and made of a material of resistivity 120 Ωm.
A1920B4.8C2.4D960Find the resistance (in mega Ω ) of a wire of length 20 m, cross sectional area 1 cm 2 and made of a material of resistivity 200 Ωm.
A40B4000C80D2000
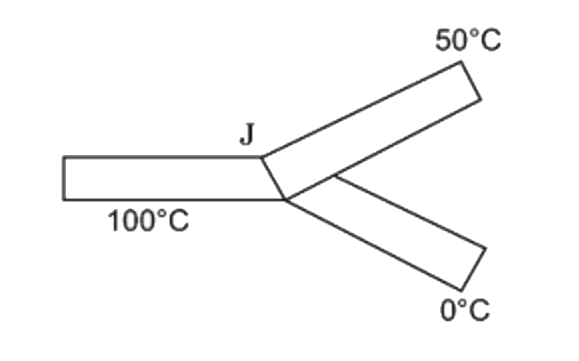
Three rods of same dimensions have thermal conductivities 3K, 2k and K, with their ends at 100∘C,50∘Cand0∘C respectively . They re arranged as shown in the diagram . The temperature of the junction J in steady -state is
View SolutionA bar of copper of length 75 cm and a bar of steel of length 125 cm are joined together end to end . Both are of circular cross - section with diameter 2 cm . The free ends of the copper and steel bars are maintained at 100∘C and 0∘C respectively . The surface of the bars are thermally insulted . What is the temperature of the copper - steel junction ? What is the heat transmitted per unit time across the junction ? Thermal conductivty of copper 9.2×10−2kcalm−1∘C−1s−1 and that of steel is 1.1×10−2kcalm−1s−1(∘)C−1.
View Solution+2.0 -0.0 An engineer joined a rod in which 50 cm is copper and 100 cm is steel from end to end together. Both have the circular cross-section with diameter 3 cm. If the free end of copper and steel are maintained at the temperature 100°C and 0°C respectively. Determine the temperature of the copper-steel junction. (Assume the thermal conductivity of copper and steel are 386 J/m - 5-°C. 46 J/m - 5-°C respectively) 50 cm 100 cm 100°C Copper Steel 0°C
View SolutionThree identical rods are joined in series as shown. Their thermal conductivities are K,K/2 and K/3 respectively. At steady, if the free ends of rods are at 100∘C and 20∘C respectively. Determine the temperature at two junction points. Also find the equivalent thermal conductivity.
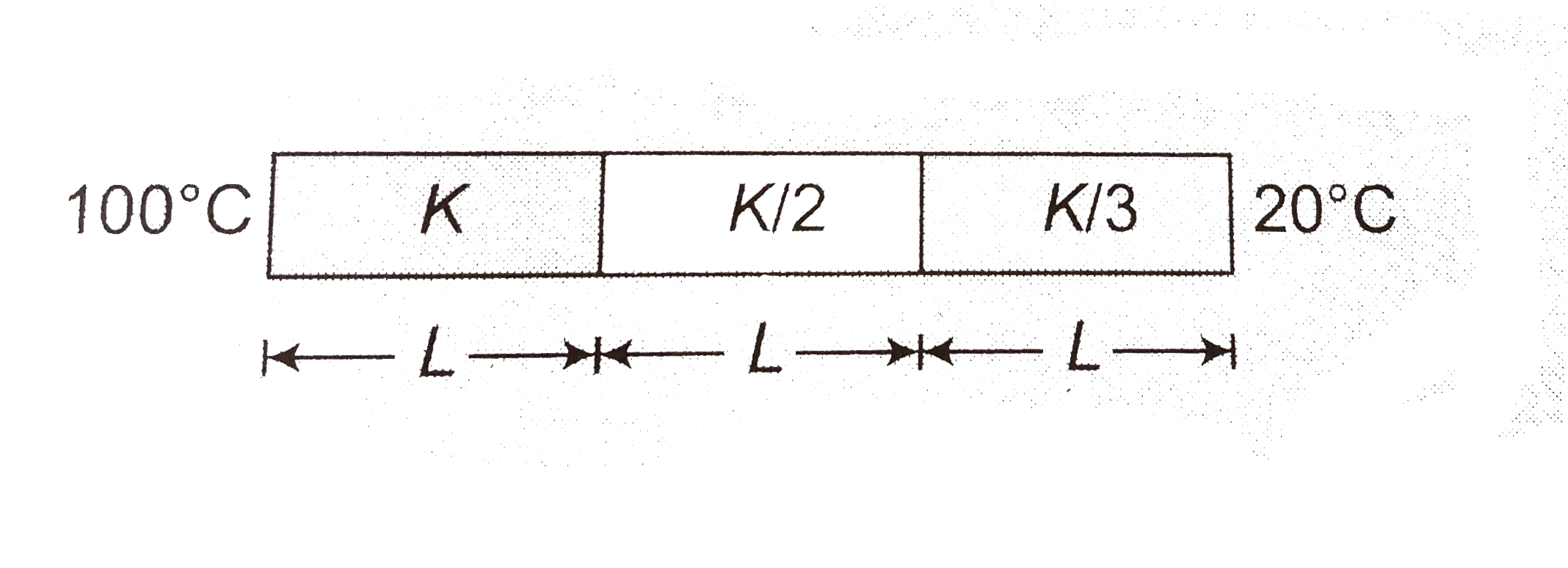
View SolutionCylinder copper rod of length 1m and a cylinder steel rod of length 1.5m are joined together end to end. The cross sectional area of eac rod is 3.14cm. The free ends of steel rod and copper rods are maintained at 0∘C and 100∘C respectively. The surfaces of rods are thermally insulated. Find the temperature of copper steel junction. (Given thermal conductivity of steel =46J/m−s.∘C and the thermal conductivity of copper =386J/m−s.∘C)
View Solution
