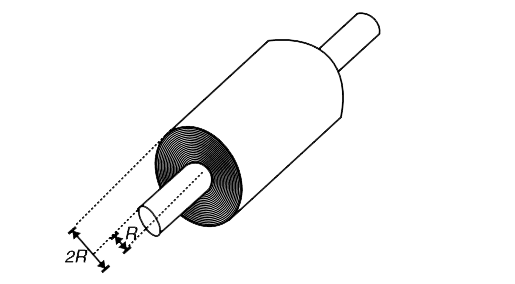
A carpet of mass is rolled along its length so as to from a cylinder of radius and is kept on a rough floor. When a negligibly small push is given to the cylindrical carpet, it stars unrolling itself without sliding on the floor. Calculate horizontal velocity of cylindrical part of the carpet when its radius reduces to .
If is the density of the material of the carpet, initial mass of the carpet (cylinder) M will be while when its radius becomes half the mass of cylindrical part will be So intial PE of the carpet is MgR while final So loss in potential energy when due to unrolling radius changes from R to R/2 = MgR — (1/ 8)MgR = (7 /8)MgR (i)This loss in potential energy is equal to increase in rotational KE which is If vis the velocity when half the carpet has unrolled then as i.e., So from Equation (i) and (ii) =(7/8)MgR Ans.
Similar Questions
A carpet of mass M is rolled along its length so as to from a cylinder of radius R and is kept on a rough floor. When a negligibly small push is given to the cylindrical carpet, it stars unrolling itself without sliding on the floor. Calculate horizontal velocity of cylindrical part of the carpet when its radius reduces to R/2.
View SolutionA bullet of mass m moving with a velocity of u just grazes the top of a solid cylinder of mass M and radius R resting on a rough horizontal surface as shown and is embedded in the cylinder after impact. Assuming that the cylinder rolls without slipping, find the angular velocity of the cylinder and the final velocity of the bullet.

View Solution
Knowledge Check
A floor-mat of mass M made up of extensible material, is rolled along its length so as to form a cylinder of radius R and kept on a rough horizontal surface. If the mat is now unrolled, without sliding, to a radius R2, the decrease in potential energy is
A25MgRB57MgRC78MgRDMgRA solid cylinder of mass M and radius R rolls without slipping on a flat horizontal surface. Its moment of inertia about the line of contact is ?
AMR22BMR2C32MR2D2MR2A particle of mass M is moving in a horizontal circle of radius R with uniform speed V. When it moves from one point to a diametrically opposite point , its
AKinetic energy changes by MV2/4Bmomentum does not changeCMomentum changes by 2MVDkinetic energy changes by MV2
A sphere of mass m and radius R is kept on a rough floor. A sharp impulse is applied in the horizontal direction at the height of centre of sphere so that sphere acquires a linear velocity v0 without any angular velocity. Calculate the velocity of sphere when pure rolling starts.
View SolutionA cylinder of mass m and radius R is kept on a rough surface after giving its centre a horizontal speed v0. Find the speed of the centre of the cylinder when it stops slipping.
View SolutionA uniform rod of maass m and length L is placed on the fixed cylindrical surface of radius R at an small angular position θ from the vertical (vertical means line joining centre and vertex of the cylindrical path) as shown in the figure and released from rest. Find the angular velocity ω of the rod at the instant when it crosses the horizontal position (Assume that when rod comes at horizontal position its mid point and vertex of the circular surface coincide). Friction is sufficient to prevent any slipping.

View SolutionA thin carpet of mass 2m is rolled over a hollow cylinder of mass m. The cylinder wall is thin and radius of the cylinder is R. The carpet rolled over it has outer radius 2R (see figure). This roll is placed on a rough horizontal surface and given gentle push so that the carpet begins to roll and unwind. Friction is large enough to prevent any slipping of the carpet on the floor. Also assume that the carpet does not slip on the surface of the cylinder. The entire carpet is laid out on the floor and the hollow cylinder rolls out with speed V. Find V.
View SolutionA particle of mass M is moving in a horizontal circle of radius R with uniform speed V. When it moves from one point to a diametrically opposite point, its
View Solution