A cylinder of mass m and radius R is kept on a rough surface after giving its centre a horizontal speed v0. Find the speed of the centre of the cylinder when it stops slipping.
F.B.D. of the cylinder is as follows :
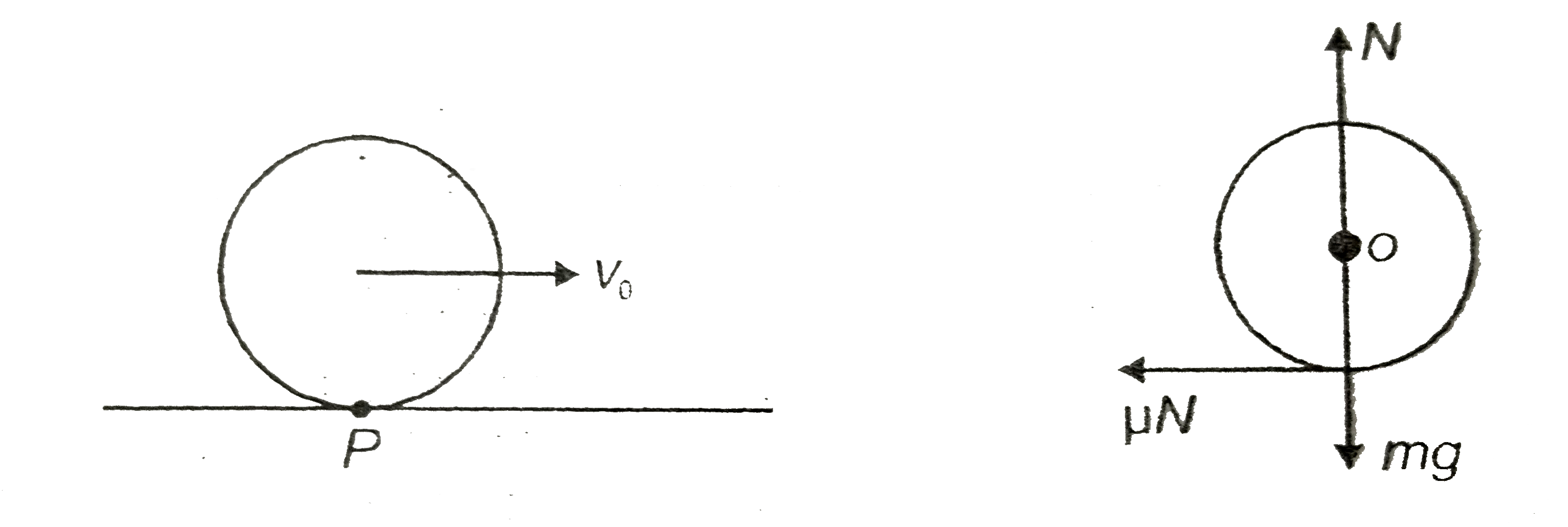
The torque of all the forces about point of contact P is zero.
∑τp=0
∴ Angular momentum remains conserved about axis passing through point P
Li=mvCMr⊥+ICMω
=mv0⋅R+mR22⋅0=mv0R (clockwise)
Lf=mvCM⋅r⊥+ICM⋅ω
=m.v.R+mR22⋅ω (since in pure rolling v=ωR)
=mvR+mR22⋅vR=32mvR
Li=Lf
or mv0R=32mvR
=2v03
Topper's Solved these Questions
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBOOK - AAKASH INSTITUTECHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Illustration
4 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBOOK - AAKASH INSTITUTECHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Assignment (Section - A) Objective Type Questions (One option is correct)
62 Videos
- SEMICONDUCTOR ELECTRONICS: MATERIALS, DEVICES AND SIMPLE CIRCUITSBOOK - AAKASH INSTITUTECHAPTER - SEMICONDUCTOR ELECTRONICS: MATERIALS, DEVICES AND SIMPLE CIRCUITSEXERCISE - Assignment (Section-D (Assertion and reason))
5 Videos
- TEST 1BOOK - AAKASH INSTITUTECHAPTER - TEST 1EXERCISE - EXERCISE
9 Videos
Similar Questions
A bullet of mass m moving with a velocity of u just grazes the top of a solid cylinder of mass M and radius R resting on a rough horizontal surface as shown and is embedded in the cylinder after impact. Assuming that the cylinder rolls without slipping, find the angular velocity of the cylinder and the final velocity of the bullet.

View Solution
A uniform cylinder of mass M and radius R is released from rest on a rough inclined surface of inclination θ with the horizontal as shown in figure. As the cylinder rolls down the inclined surface, the maximum elongation it the spring stiffness k is
View Solution
Knowledge Check

A uniform solid cylinder of mass m and radius R is placed on a rough horizontal surface. A horizontal constant force F is applied at the top point P of the cylinder so that it start pure rolling. The acceleration of the cylinder isAF/3mB2F/3mC4F/3mD5F/3mA solid cylinder of mass M and radius R rolls from rest down a plane inclined at an angle θ to the horizontal. The velocity of the centre of mass of the cylinder after it has rolled down a distance d is :
A√23gdtanθB√gdtanθC√34gdsinθD√43gdsinθA solid sphere of mass M and radius R is placed on a smooth horizontal surface. It is given a horizontal impulse J at a height h above the centre of mass and sphere starts rolling then, the value of h and speed of centre of mass are –
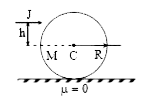 Ah=25Randv=JMBh=25Randv=25JMCh=75Randv=75JMDh=75Randv=JM
Ah=25Randv=JMBh=25Randv=25JMCh=75Randv=75JMDh=75Randv=JM
A cylinder of mass M, radius R is kept on a rough horizontal plane at one extreme end of the platfonn at t = 0. Axis of the cylinder is parallel to z-axis. The platform is oscillating in the xy-plane and its displacement from origin is represented by x = 4 cos(2πt) metres. There is no slipping between the cylinder and the platfonn. Find the acceleration of the centre of mass of cylinder at t =16s
(##TRG_PHY_MCQ_XII_C04_E04_001_Q01.png" width="80%">
View SolutionA solid cylinder of mass M and radius R rolls without slipping down an inclined plane of length L and height h. What is the speed of its centre of mass when the cylinder reaches its bottom ?
View SolutionA solid cylinder of mass M and radius R rolls without slipping down on inclined plane of length L and height h what is the speed of its centre of mass when the cylinder reaches its bottom?
View SolutionA solid cylinder of mass M and radius R rolls without slipping down on inclined plane of length L and height h what is the speed of its centre of mass when the cylinder reaches its bottom?
View SolutionA solid cylinder of mass M and radius R rolls without slipping down an inclined plane of length L and height h. What is the speed of its center of mass when the cylinder reaches its bottom
View Solution