An infinite line charge is at the axis of a cylinder of length 1 m and radius 7 cm. If electric field at any point on the curved surface of cylinder is 250 NC−1, then net electric flux through the cylinder is
1.1×102 Nm2C−1
9.74×10−6 Nm2C−1
5.5×106 Nm2C−1
2.5×102 Nm2C−1
The correct Answer is:A
To find the net electric flux through the cylinder due to an infinite line charge at its axis, we can follow these steps:
1. Identify Given Values:
- Length of the cylinder, L=1m
- Radius of the cylinder, r=7cm=0.07m
- Electric field at the curved surface, E=250N/C
2. Understand Electric Flux:
- The electric flux Φ through a surface is given by the formula:
Φ=E⋅A⋅cos(θ)
- Where E is the electric field, A is the area through which the field lines pass, and θ is the angle between the electric field and the normal to the surface.
3. Calculate the Area of the Curved Surface:
- The area A of the curved surface of the cylinder is given by:
A=2πrL
- Substituting the values:
A=2π(0.07m)(1m)=2π(0.07)≈0.4398m2
4. Calculate the Electric Flux through the Curved Surface:
- Since the electric field is radially outward and the area vector of the curved surface is also outward, the angle θ=0∘ (which means cos(0)=1).
- Therefore, the electric flux through the curved surface is:
Φcurved=E⋅A⋅cos(0)=E⋅A
- Substituting the values:
Φcurved=250N/C⋅0.4398m2≈109.95N m2/C
5. Final Result:
- The net electric flux through the cylinder is approximately:
Φ≈1.1×102N m2/C
- Length of the cylinder, L=1m
- Radius of the cylinder, r=7cm=0.07m
- Electric field at the curved surface, E=250N/C
- The electric flux Φ through a surface is given by the formula:
Φ=E⋅A⋅cos(θ)
- Where E is the electric field, A is the area through which the field lines pass, and θ is the angle between the electric field and the normal to the surface.
- The area A of the curved surface of the cylinder is given by:
A=2πrL
- Substituting the values:
A=2π(0.07m)(1m)=2π(0.07)≈0.4398m2
- Since the electric field is radially outward and the area vector of the curved surface is also outward, the angle θ=0∘ (which means cos(0)=1).
- Therefore, the electric flux through the curved surface is:
Φcurved=E⋅A⋅cos(0)=E⋅A
- Substituting the values:
Φcurved=250N/C⋅0.4398m2≈109.95N m2/C
- The net electric flux through the cylinder is approximately:
Φ≈1.1×102N m2/C
Similar Questions
Knowledge Check
a point charge q is placed at the centre of a cylinder of length L and radius R the electric flux through the curved surface of the cylinder is
Aqε0L√L2+R2Bqε0L√L2+2R2Cqε0L√L2+4R2Dq2ε0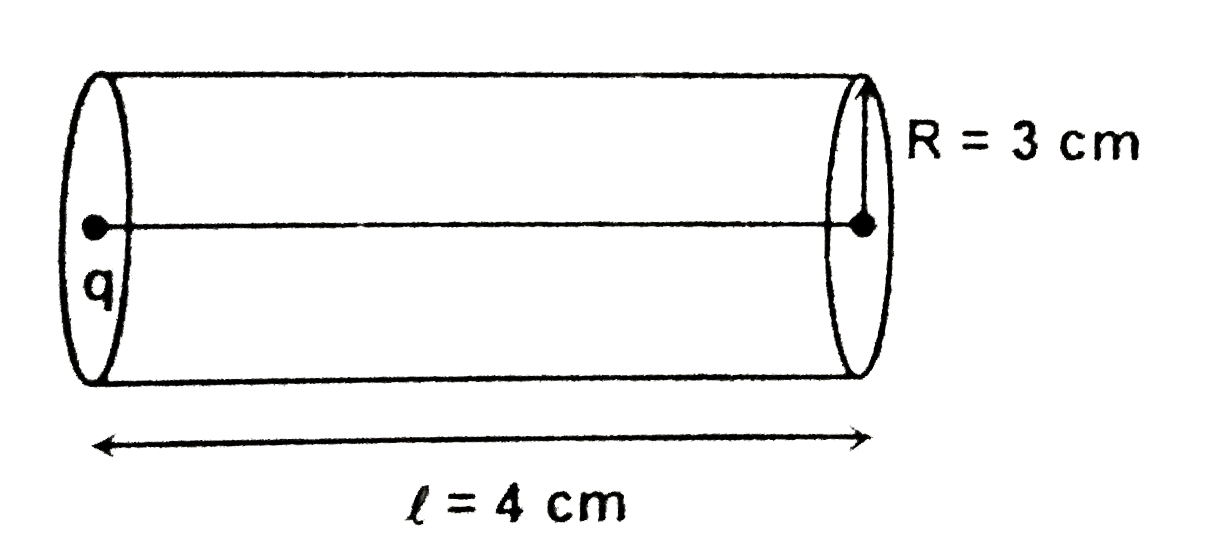
A point charge 'q' is placed at the centre of left circular end of a cylinder of length l=4cm and radius R=3 cm shown. Then the electric flux through the curved surface of the cylinder isAq5ε0B2q5ε0C3q5ε0D4q5ε0A cylinder of radius R and length l is placed in a uniform electric field E parallel to the axis of the cylinder. The total flux over the curved surface of the cylinder is
AzeroBπR2EC2πR2EDE/πR2
A cylinder of radius r and length l is placed in an uniform electric field parallel to the axis of the cylinder. The total flux for the surface of the cylinder is given by-
View SolutionA hollow cylinder of length L and radius R having surface area A is placed horizontally with its axis parallel to an external field E. The electric flux through the surface of the cylinder is
View SolutionA hollow cylinder of length L and radius R having surface area A is placed horizontally with its axis parallel to an external field E. The electric flux through the surface of the cylinder is
View SolutionA cylinder of length L has a charge of magnitude q. The electric intensity at a point at a distance r from the axis of the cylinder is
View SolutionIf the linear charge density of a cylinder is 4μCm−6 ,then electric field intensity at point 3.6 cm from axis is :
View Solution

