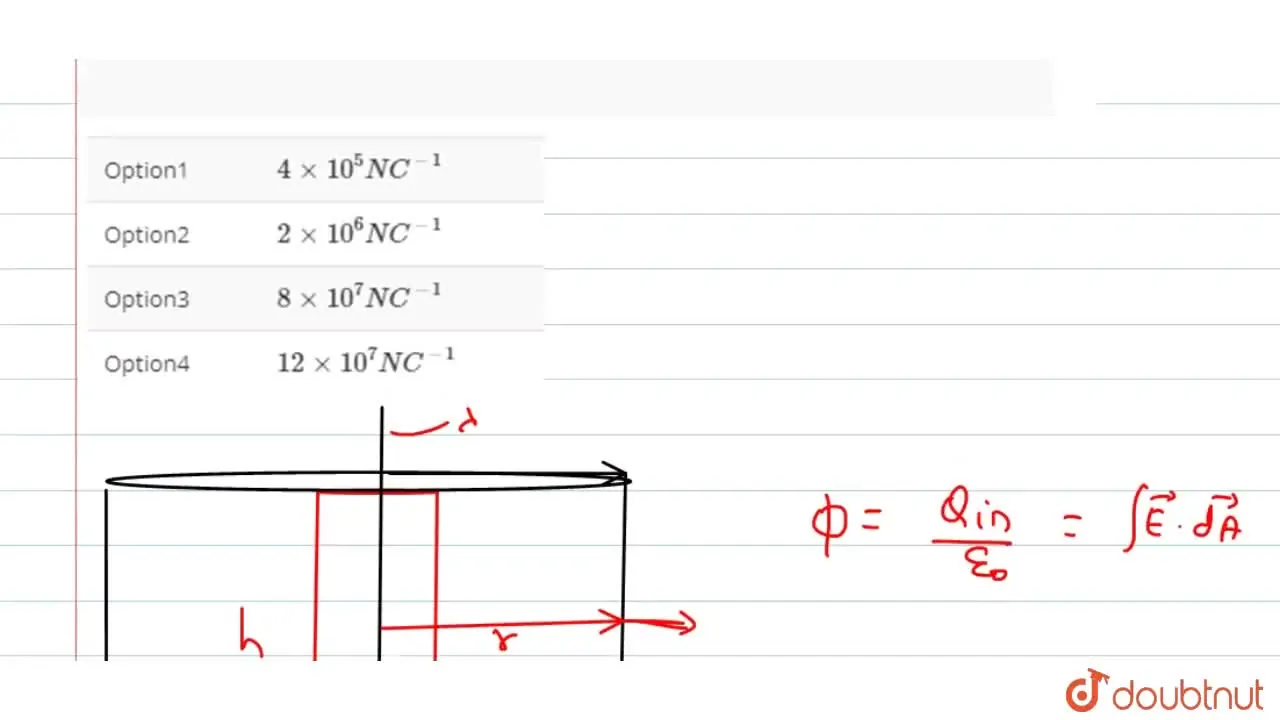
If the linear charge density of a cylinder is 4μCm−6 ,then electric field intensity at point 3.6 cm from axis is :
4×105NC−1
2×106NC−1
8×107NC−1
12×107NC−1
The correct Answer is:B
Use E=λ2πe0r and put values to get E=2×106Ne−1
Similar Questions
A thin long conductor has linear charge density of 20 μC/m. Calculate the electric field intensity at a point 5 cm from it. Draw a graph to show variation of electric field intensity with distance from the conductor.
View SolutionAn infinitely long cylindrical shell ofinner radius r1 and outer radius r2 is charged in its volume with a volume charge density which varies with distance from axis of cylinder as p=blrC/m3 which C is a positive constant and r is the distance from axis of cylinder. Find the electric field intensity at a point P at a distance x from axis of cylinder
View SolutionAn infinitely long thin straight wire has uniform linear charge density of 1/3coulm−1 .Then the magnitude of the electric intensity at a point 18cm away is
View SolutionIf σ is surface density of charge on the charged cylinder of radius R, then electric intensity E at outer point at a distance r from its axis is
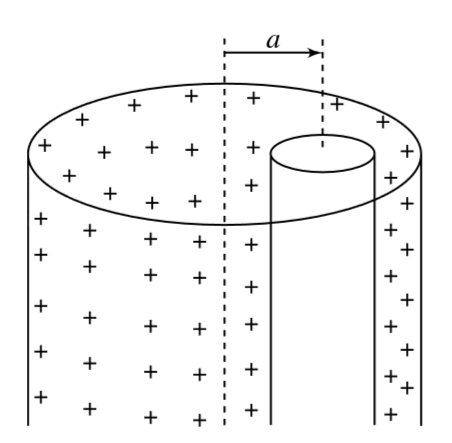
View Solution(a) There is a long uniformly charged cylinder having a volume charge density of ρC/m3. Radius of the cylinder is R. Find the electric field at a point at a distance x from the axis of the cylinder for following cases (i) x lt R (ii) x gt R What is the maximum field produced by the charge distribution at any point? (b) The cylinder described in (a) has a long cylindrical cavity. The axis of cylindrical cavity is at a distance a from the axis of the charged cylinder (see figure). Find electric field inside the cavity.
 View Solution
View SolutionA very long uniformly charged cylinder (radius R) has a surface charge density σ . A very long uniformly charged line charge( linear charge density λ) is placed along the cylinder axis. If electric field intensity vector outside the cylinder is zero then :
View SolutionA plane conductor with very large dimensions is charged such that surface charge density is 1.6×10−2C/m2. The electric field intensity at a point near it if the conductor is in a medium of dielectric constant 5 is
View SolutionFor a point situated at a distance 20 cm from the axis of a long cyclindrical charged conductor, the electric intensity is 0.4N/C . The electric intensity at another point situated at 4o cm from the axis is
View SolutionAn infinitely long uniform linear charge distribution has a charge density 4 μC/m. what is the electric field at a point at a perpendicular distance of 3.6 cm from the line? Given: 14πε0=9×109Nm2/C2
View SolutionFor an infinitely long metal cylinder, the radius is 3 mm, K=6.28 annd charge density=4μC/m2. What is the electric intensity (E) at a distance of 1.5 m from the axis? [14πε0=9×109]
View Solution