An infinitely long thin straight wire has uniform linear charge density of 1/3coulm−1 .Then the magnitude of the electric intensity at a point 18cm away is
0.33×1011N/C
3×1011NC−1
0.66×1011NC−1
1.32×1011NC−1
The correct Answer is:1
To find the magnitude of the electric field intensity at a point 18 cm away from an infinitely long thin straight wire with a uniform linear charge density of λ=13C/m, we can use the formula for the electric field due to an infinite line charge.
1. Identify the Given Values:
- Linear charge density, λ=13C/m
- Distance from the wire, r=18cm=0.18m
2. Use the Formula for Electric Field:
The electric field E due to an infinitely long line charge is given by the formula:
E=2kλr
where k is Coulomb's constant, approximately k=9×109N m2/C2.
3. Substitute the Values into the Formula:
E=2×(9×109)×(13)0.18
4. Calculate the Electric Field:
- First, calculate 2×9×109:
2×9×109=18×109
- Now substitute this into the equation:
E=18×109×130.18
- Simplify 183=6:
E=6×1090.18
- Now calculate 6×1090.18:
E=33.33×109N/C
5. Final Result:
The magnitude of the electric field intensity at a point 18 cm away from the wire is:
E≈3.33×1010N/C
- Linear charge density, λ=13C/m
- Distance from the wire, r=18cm=0.18m
The electric field E due to an infinitely long line charge is given by the formula:
E=2kλr
where k is Coulomb's constant, approximately k=9×109N m2/C2.
E=2×(9×109)×(13)0.18
- First, calculate 2×9×109:
2×9×109=18×109
- Now substitute this into the equation:
E=18×109×130.18
- Simplify 183=6:
E=6×1090.18
- Now calculate 6×1090.18:
E=33.33×109N/C
The magnitude of the electric field intensity at a point 18 cm away from the wire is:
E≈3.33×1010N/C
Topper's Solved these Questions
- ELECTROSTATICS AND GAUSS LAWBook:NARAYNAChapter:ELECTROSTATICS AND GAUSS LAWExercise:Level 3
Explore 22 Videos
- ELECTROSTATICS AND GAUSS LAWBook:NARAYNAChapter:ELECTROSTATICS AND GAUSS LAWExercise:NCERT based Question
Explore 14 Videos
- ELECTROSTATICS AND GAUSS LAWBook:NARAYNAChapter:ELECTROSTATICS AND GAUSS LAWExercise:Level 1
Explore 8 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCEBook:NARAYNAChapter:ELECTROSTATIC POTENTIAL AND CAPACITANCEExercise:ADDITIONAL PROBLEMS
Explore 14 Videos
- EXPERIMENTAL PHYSICSBook:NARAYNAChapter:EXPERIMENTAL PHYSICSExercise:Comprehension type
Explore 6 Videos
Similar Questions
An infinitely thin straight wire has uniform linear charge density λ . Obtain the expression. For the electric field (E) at a point lying at a distance x from the wire, using Gauss' law.
(b) Show graphically the variation of this electric field E as a function of distance x from the wire .
View SolutionAn infinitely long time charge has linear charge density λC/m the line charge is along the line x=0,z=2m find the electric field at point (1,1,1) m.
View Solution
Knowledge Check
If the linear charge density of a cylinder is 4μCm−6 ,then electric field intensity at point 3.6 cm from axis is :
A4×105NC−1B2×106NC−1C8×107NC−1D12×107NC−1Two infinitely long thin styraight wires having uniform linear charge densities λ and 2λ are arranged parallel to each other at a distance r apart.The intensity of the electric field at a point midway between them is
A2λπε0Bλπε0rCλ2πε0rD3λ2πε0rA positively charged infinitely long cylinder has a radius of 0.1 m and surface charge density of 8.85×10−12C/m2. What is the intensity of the electric field at a point on the surface of the cylinder, if the cylinder is kept in vacuum?
A0.5 V/mB1 V/mC1.5 V/mD2 V/m
Figure shows a long wire having uniform charge density λ as shown in figure. Calculate electric field intensity at point P.
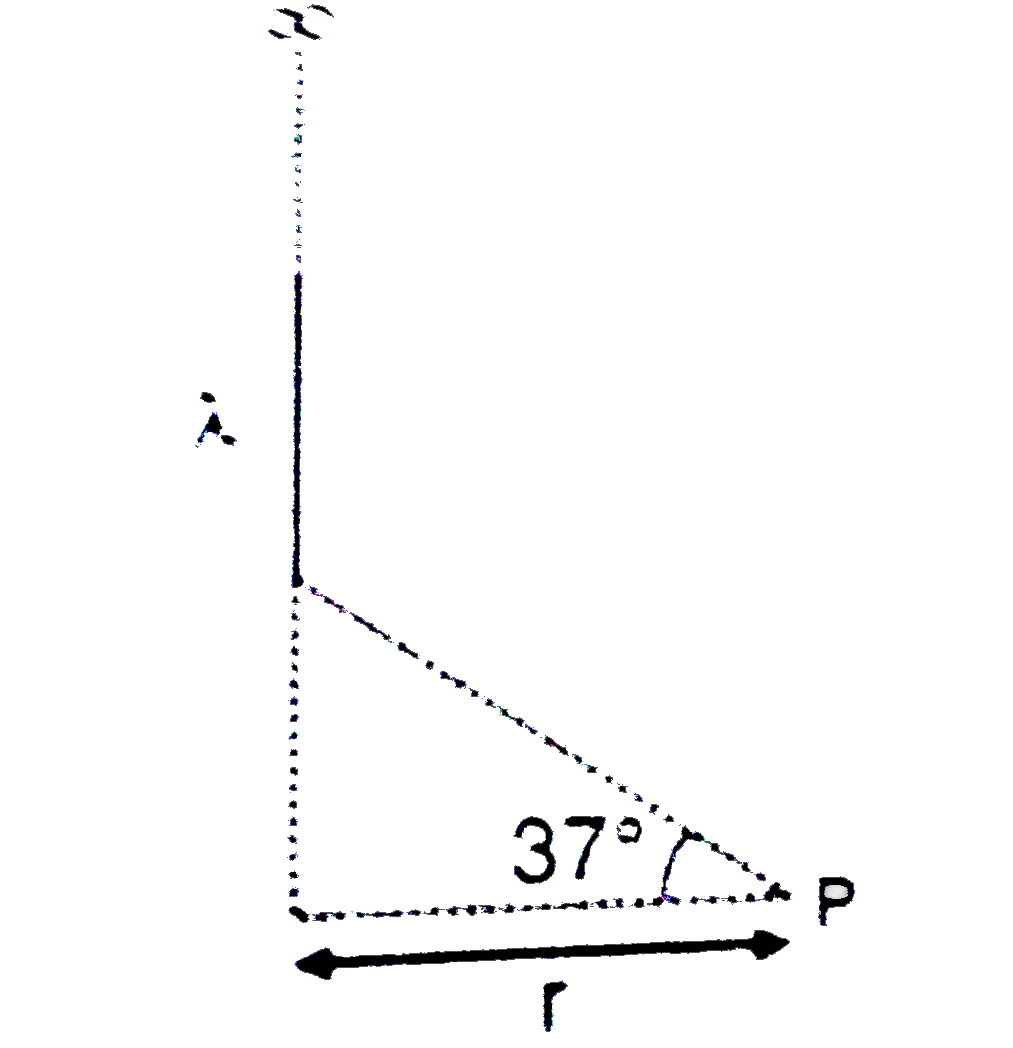
View SolutionA long wire with a uniform charge density λ is bent in two configurations shown in fig. Determine the electric field intensity at point O.
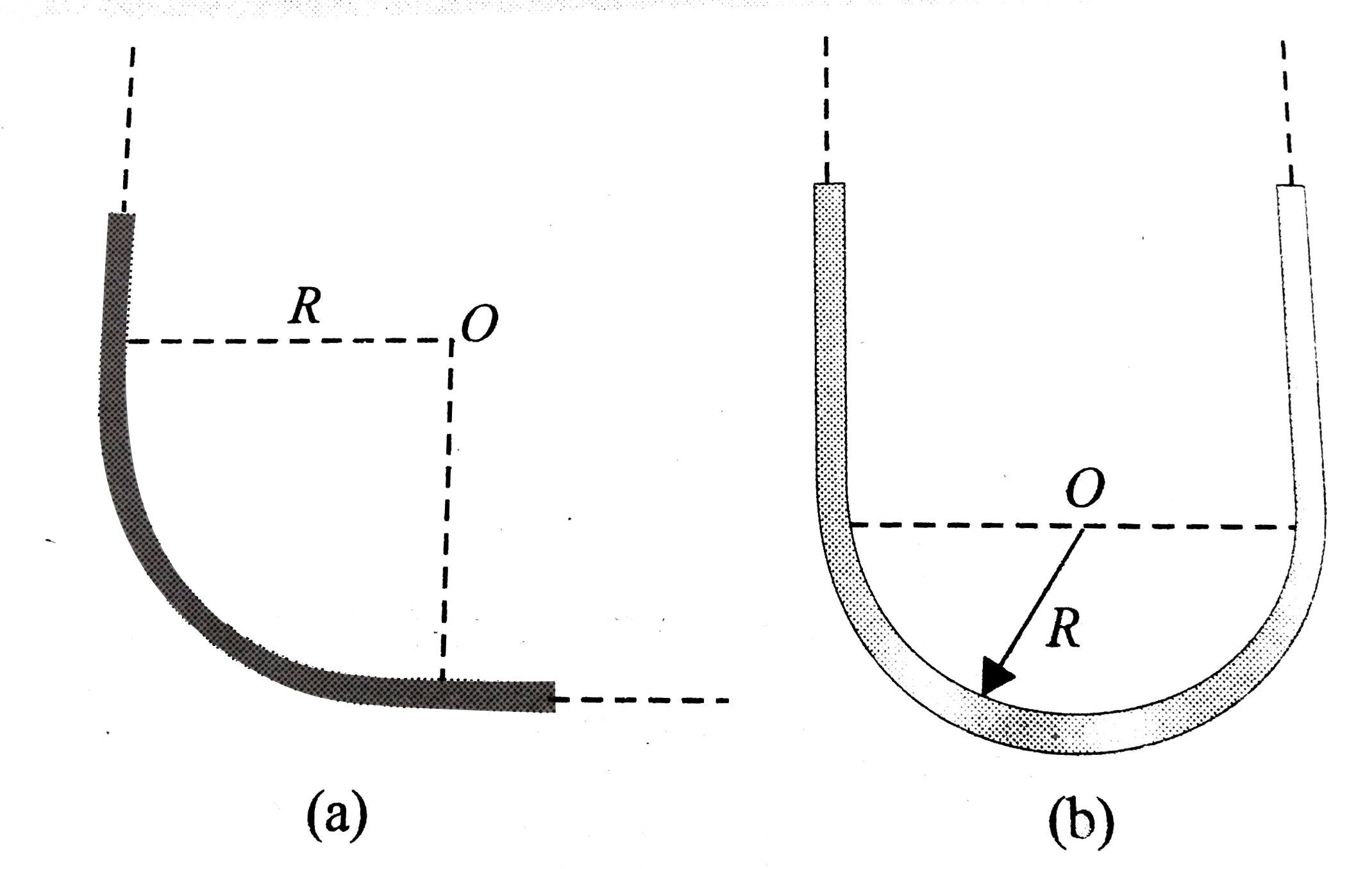
View SolutionAn equilaterial triangle ABC has a side a. Two infinitely long thin straight wires having uniform linear charge densities ' lamda ' and '-lamda' are arranged at A and B perpendicular to the plante of the triangle. The magnitude of electric intensity at the third vertex c will be
View SolutionIf a long straight wire carries a current of 40 A, then the magnitude of the field B at a point 15 cm away from the wire is
View SolutionAn infinitely long wire is kept along z-axis from z=−∞ to z=+∞, having uniform linear cahrges density 109nC/m. The electric field at point (6cm,8cm,10cm) will be
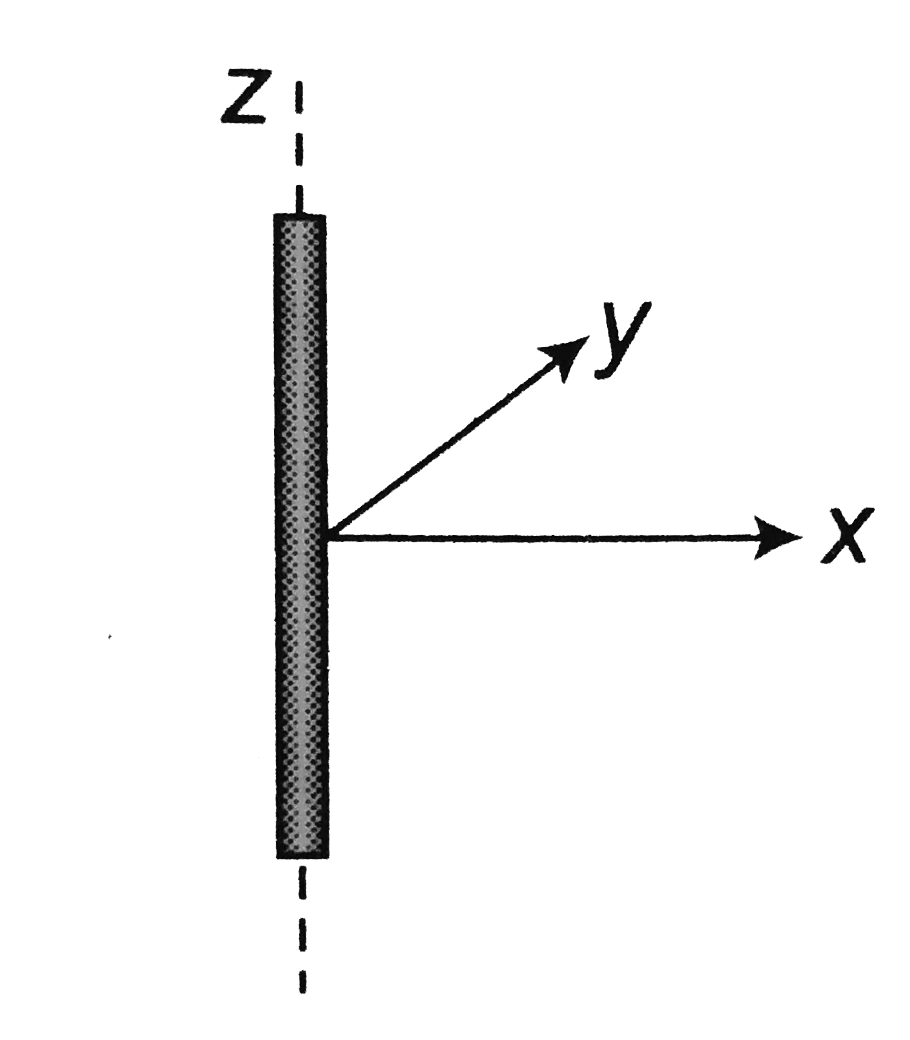
View Solution

