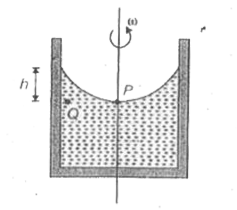
A cylindrical vessel of radius r containing a liqiud is rotating about a vertical axis through the centre of circular base, If the vessel is rotating with angular velocity $ω$ then what is the difference of the heights of liquid at centre of vessel and edge?

Video Solution

Text Solution

Verified by Experts

When cylindrical vessel will rotate the shape of surface of liquid in the vessel is as shown in figure. Take two points P and Q in the vessel at same level as shown in figure. From Bernoulli’s theorem
$\frac{P_{P}}{ρ} + \frac{1}{2} V_{P}^{2} + g h_{P} = \frac{P_{Q}}{ρ} + \frac{1}{2} V_{Q}^{2} + g h_{Q}$
As $h_{P} = h_{Q}$ and $v_{P} = 0$
$∴ P_{P} = P_{Q} + \frac{1}{2} ρ v_{Q}^{2}$
P_(P) - P_(Q) = 1/2 rhov_(Q)
$ρ g h = \frac{1}{2} ρ r^{2} ω^{2}$
h = $\frac{r^{2} ω^{2}}{2} g$

|

Updated on:21/07/2023

Class 12 PHYSICS MECHANICAL PROPERTIES OF FLUIDS

Similar Questions

Knowledge Check

Question 1 - Select One
A liquid is kept in a cylindrical vessel which is being rotated about a vertical axis through the centre of the circular base. If the radius of the vessel is $r$ and angular velocity of rotation is $ω$ , then the difference in the heights of the liquid at the centre of the vessel and the edge is.
A $\frac{r ω}{2 g}$
B $\frac{r^{2} ω^{2}}{2 g}$
C $\sqrt{2 g r ω}$
D $\frac{ω^{2}}{2 g r^{2}}$
Question 2 - Select One
A liquid is kept in a cylindrical vessel which is being rotated about a vertical axis through the centre of the circular base. If the radius of the vessel is $r$ and angular velocity of rotation is $ω$ , then the difference in the heights of the liquid at the centre of the vessel and the edge is.
A $\frac{r ω}{2 g}$
B $\frac{r^{2} ω^{2}}{2 g}$
C $\sqrt{2 g r ω}$
D $\frac{ω^{2}}{2 g r^{2}}$
Question 3 - Select One
A rod is rotating with angular velocity $ω$ about axis AB. Find $cos θ$ .

A $\frac{g}{2 l ω^{2}}$
B $\frac{g}{l ω^{2}}$
C $\frac{2 g}{{(l ω)}^{2}}$
D $\frac{3 g}{2 l ω^{2}}$

Recommended Questions

Home
Ask Doubt
Profile