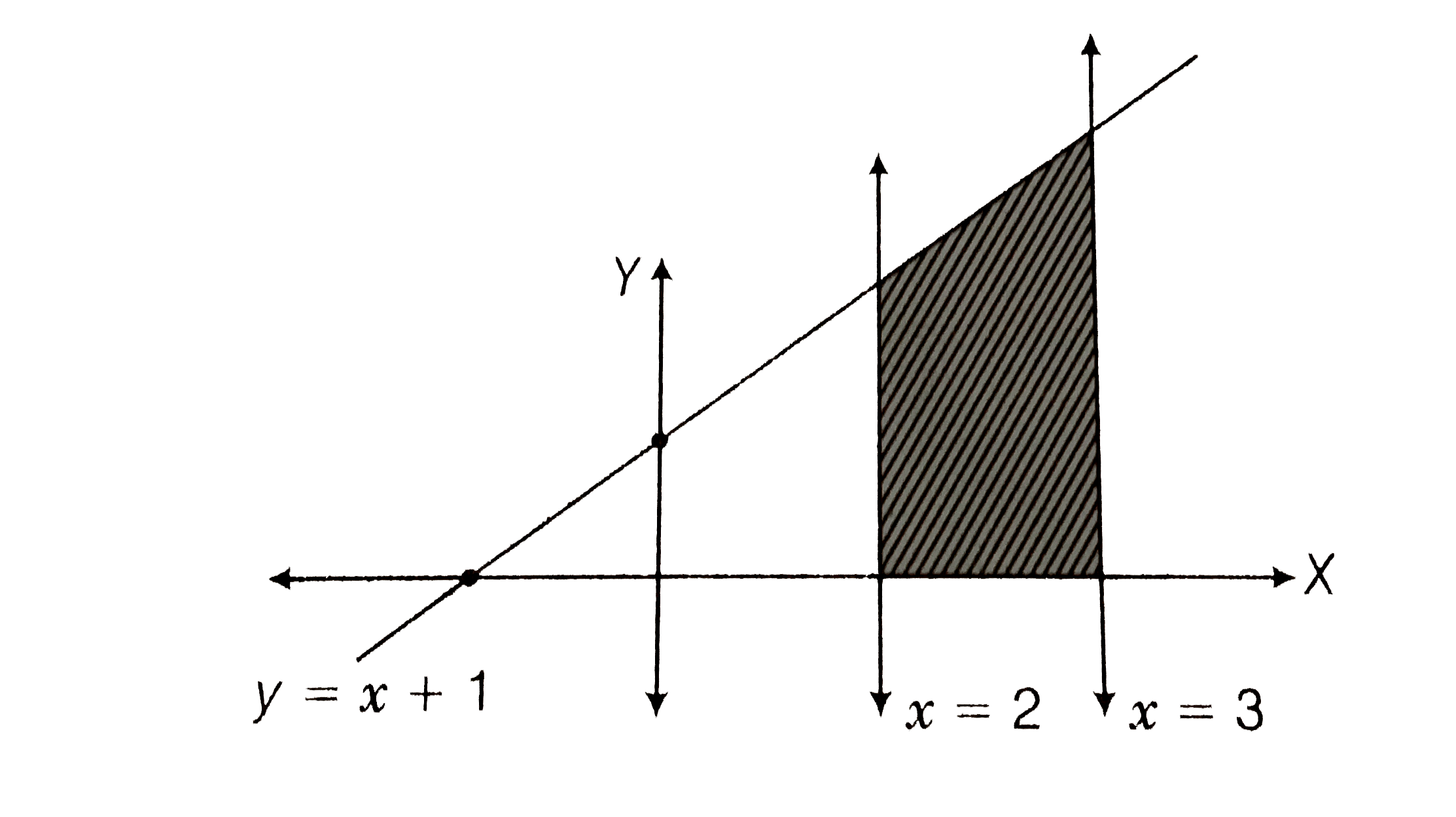
The area of the region bounded by the curve $y = x + 1$ and the lines $x = 2, x = 3,$ is

$\frac{7}{2} sq units$

$\frac{9}{2} sq unit$

$\frac{11}{2} sq unit$

$\frac{13}{2} sq units$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

Required area, $A = \int_{2}^{3} (x + 1) d x = {[\frac{x^{2}}{2} + x]}_{2}^{3}$
$= [\frac{9}{2} + 3 - \frac{4}{2} - 2] = [\frac{5}{2} + 1] = \frac{7}{2} sq units$

Updated on:21/07/2023

Class 12 MATHS APPLICATION OF INTEGRALS

Topper's Solved these Questions

APPLICATION OF DERIVATIVESBOOK - NCERT EXEMPLARCHAPTER - APPLICATION OF DERIVATIVESEXERCISE - Application Of Derivatives
64 Videos
CONTINUITY AND DIFFERENTIABILITYBOOK - NCERT EXEMPLARCHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - Continuity And Differentiability
212 Videos

Knowledge Check

The area of the region bounded by the curve $y = x^{2}$ and the line $y = 16$ is :
A $\frac{32}{3}$
B $\frac{256}{3}$
C $\frac{64}{3}$
D $\frac{128}{3}$
The area of the region bounded by the curve y=cosx, X-axis and the lines x=0, x= $2 π$ is
A2
B4
C0
D3
The area of the region bouned by the curve $y = 2 x - x^{2}$ and the line $y = x$ is
A $1 / 2$
B $1 / 3$
C $1 / 4$
D $1 / 6$

The area of the region bounded by the curve $y = 2 x - x^{2}$ and the line $y = x$ is
View Solution
Find the area of the region bounded by the curve $y^{2} = 4 x$ and the line $x = 3$ .
View Solution
Find the area of the region bounded by the curve $x y = 1$ and the lines $y = x, y = 0, x = e$
View Solution
The area of the region bounded by the curve $y = x^{3}$ , and the lines , y=8 and x=0, is
View Solution
The area of the region bounded by the curve $x = 2 y + 3$ and the lines $y = 1, y = - 1$ is
View Solution

NCERT EXEMPLAR-APPLICATION OF INTEGRALS-Application Of Integrals

The area of the region bounded by the ellipse (x^(2))/25+y^(2)/16=1 is
04:39
The area of the region by the circle x^(2)+y^(2)=1 is
03:26
The area of the region bounded by the curve y = x + 1 and the lines x=...
02:14
The area of the region bounded by the curve x=2y+3 and the lines y=1, ...
02:39
Find the area of the region bounded by the curve y^(2)=9x" and " y=3x.
02:51
Find the area of the region bounded by the parabole y^(2)=2pxx^(2)=2py...
05:23
Find the area of the region bounded by the curve y=x^(3),y=x+6" and "x...
04:17
Find the area of the region bounded by the curve y^(2)=4x" and " x^(2)...
05:22
Find the area of the region included between y^(2)=9x" and "y=x.
02:48
Find the area of the region enclosed by the parabola x^(2)=y and the l...
03:55
Find the area of the region bounded by line x = 2 and parabola y^(2)=8...
02:51
Sketch the region {(x, 0):y=sqrt(4-x^(2))} and X-axis. Find the area o...
03:38
Calculate the area under the curve y=2sqrtx included between the lines...
02:11
Using integration, find the area of the region bounded by the line 2y=...
03:38
Draw a rough sketch of the curve y=sqrtx-1) in the interval [1, 5]. Fi...
02:45
Determine the area under the curve y=sqrt(a^(2)-x^(2)) included betwee...
02:42
Find the area if the region bounded by y=sqrtx" and " y=x.
02:22
Find the area enclosed by the curve y=-x^(2) and the straight line x+y...
05:55
Find the area bounded by the curve y=sqrtx,x=2y+3 in the first quadran...
04:23
Find the area of the region bounded by the curve y^(2)=2x" and "x^(2)+...
07:03

Home
Ask Doubt
Profile

The area of the region bounded by the curve y=x+1 and the lines x=2,x=3, is

The correct Answer is:A

Required area, A=∫32(x+1)dx=[x22+x]32 =[92+3−42−2]=[52+1]=72 sq units

Topper's Solved these Questions

Similar Questions

Knowledge Check

The area of the region bounded by the curve y=x2 and the line y=16 is :

The area of the region bounded by the curve y=cosx, X-axis and the lines x=0, x=2π is

The area of the region bouned by the curve y=2x−x2 and the line y=x is

NCERT EXEMPLAR-APPLICATION OF INTEGRALS-Application Of Integrals

The area of the region bounded by the curve $y = x + 1$ and the lines $x = 2, x = 3,$ is

Required area, $A = \int_{2}^{3} (x + 1) d x = {[\frac{x^{2}}{2} + x]}_{2}^{3}$
$= [\frac{9}{2} + 3 - \frac{4}{2} - 2] = [\frac{5}{2} + 1] = \frac{7}{2} sq units$

The area of the region bounded by the curve $y = x^{2}$ and the line $y = 16$ is :

The area of the region bounded by the curve y=cosx, X-axis and the lines x=0, x= $2 π$ is

The area of the region bouned by the curve $y = 2 x - x^{2}$ and the line $y = x$ is