A particle moves along x - axis in such a way that its x - co - ordinate varies with time according to the equation x=4−2t+t2. The speed of the particle will vary with time as
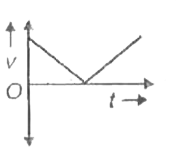

The correct Answer is:B
To solve the problem, we need to find the speed of the particle as a function of time given the position function x(t)=4−2t+t2.
1. Identify the Position Function:
The position of the particle as a function of time is given by:
x(t)=4−2t+t2
2. Differentiate the Position Function:
To find the speed of the particle, we need to compute the derivative of the position function with respect to time t. This derivative gives us the velocity v(t):
v(t)=dxdt=ddt(4−2t+t2)
3. Calculate the Derivative:
- The derivative of the constant 4 is 0.
- The derivative of −2t is −2.
- The derivative of t2 is 2t.
Therefore, the velocity function becomes:
v(t)=0−2+2t=2t−2
4. Determine the Speed:
Speed is the absolute value of velocity. Thus, the speed s(t) is given by:
s(t)=|v(t)|=|2t−2|
5. Analyze the Speed Function:
The expression |2t−2| indicates that the speed will vary depending on the value of t:
- For t<1, 2t−2<0 so s(t)=−(2t−2)=2−2t.
- For t=1, s(t)=0.
- For t>1, 2t−2>0 so s(t)=2t−2.
Final Expression for Speed:
Thus, the speed of the particle varies with time as:
s(t)=|2t−2|
The position of the particle as a function of time is given by:
x(t)=4−2t+t2
To find the speed of the particle, we need to compute the derivative of the position function with respect to time t. This derivative gives us the velocity v(t):
v(t)=dxdt=ddt(4−2t+t2)
- The derivative of the constant 4 is 0.
- The derivative of −2t is −2.
- The derivative of t2 is 2t.
Therefore, the velocity function becomes:
v(t)=0−2+2t=2t−2
Speed is the absolute value of velocity. Thus, the speed s(t) is given by:
s(t)=|v(t)|=|2t−2|
The expression |2t−2| indicates that the speed will vary depending on the value of t:
- For t<1, 2t−2<0 so s(t)=−(2t−2)=2−2t.
- For t=1, s(t)=0.
- For t>1, 2t−2>0 so s(t)=2t−2.
Thus, the speed of the particle varies with time as:
s(t)=|2t−2|
Topper's Solved these Questions
- MOTION IN A STRAIGHT LINEBook:AAKASH INSTITUTEChapter:MOTION IN A STRAIGHT LINEExercise:ASSIGNMENT (SECTION - B)
Explore 33 Videos
- MOTION IN A STRAIGHT LINEBook:AAKASH INSTITUTEChapter:MOTION IN A STRAIGHT LINEExercise:ASSIGNMENT (SECTION - C)
Explore 37 Videos
- MOTION IN A STRAIGHT LINEBook:AAKASH INSTITUTEChapter:MOTION IN A STRAIGHT LINEExercise:EXERCISE
Explore 30 Videos
- MOTION IN A PLANEBook:AAKASH INSTITUTEChapter:MOTION IN A PLANEExercise:Assignement section -J (Aakash Challengers Questions)
Explore 4 Videos
- MOTION IN STRAIGHT LINEBook:AAKASH INSTITUTEChapter:MOTION IN STRAIGHT LINEExercise:Assignment (SECTION - J)
Explore 2 Videos
Similar Questions
A particle moves along the X-axis. Its X-coordinate varies with time according to the expression x=4t+2r2, where x is in meters and t is in seconds. The position-time graph for this motion is shown in the figures previously. Note that the particle moves in the negative X-direction for the first second of motion, is at rest at the moment t=1s, and then heads back in the positive X-direction for t>1s.
Find the displacement of the particle in the time interval t=1sto t=3s.
View SolutionA particle moves along x axis in such a way that its coordinate x varies with time t according to the equation x=A0−A1t+A2t2. The initial velocity of the particle is.
View Solution
Knowledge Check
A particle moves along x-axis in such a way that its x-coordinate varies with time t according to the equation x=(8−4t+6t2) metre.
The velocity of the particle will vary with time according to the graph :-A B
B C
C D
D
A particle moves along x-axis in such a way that its r-coordinate varies with time't according to the equation x= (8−4t+6t2) metre. The velocity of the particle will vary with time according to the graph
A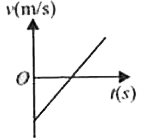 B
B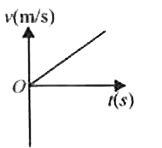 C
C D
D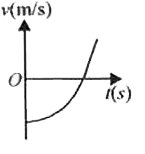
A particle moves along X-axis in such a way that its coordinate X varies with time t according to the equation x=(2−5t+6t2)m. The initial velocity of the particle is
A−5m/sB6m/sC−3m/sD3m/s
A particle moves along the x-axis in such a way that its x-co-ordinate varies with time as x=2–5t+6t2.
The initial velocity and acceleration of particle will respectively be-
View SolutionA particle moves in an XY-plane in such a way that its x and y-coordinates vary with time according to
x(t)=t3−32t,y(t)=5t2+12
Find the acceleration of the particle, if t = 3 s.
View SolutionA particle moves along the x-axis such that its co-ordinate (x) varies with time (t), according to the expression x=2−5t+6t2, where x is in metres and t is in seconds. The initial velocity of the particle is :–
View SolutionA particle moves a distance x in time t according to equation x2=1+t2 . The acceleration of the particle is
View SolutionA particle moves in the x-y plane. It x and y coordinates vary with time t according to equations x=t2+2t and y=2t. Possible shape of path followed by the particle is
View Solution

