A particle moves along X-axis in such a way that its coordinate X varies with time t according to the equation x=(2−5t+6t2)m. The initial velocity of the particle is
−5m/s
6m/s
−3m/s
3m/s
The correct Answer is:A
To find the initial velocity of the particle, we need to follow these steps:
1. Understand the equation of motion: The position of the particle as a function of time is given by the equation:
x(t)=2−5t+6t2
2. Differentiate the position function: The velocity of the particle is the derivative of the position function with respect to time. We can express this mathematically as:
v(t)=dxdt
3. Calculate the derivative: We will differentiate the position function x(t):
v(t)=ddt(2−5t+6t2)
- The derivative of a constant (2) is 0.
- The derivative of −5t is −5.
- The derivative of 6t2 is 12t (using the power rule).
Therefore, we have:
v(t)=0−5+12t=−5+12t
4. Find the initial velocity: The initial velocity is the velocity at time t=0:
v(0)=−5+12(0)=−5
5. Conclusion: The initial velocity of the particle is:
v(0)=−5m/s
Final Answer:
The initial velocity of the particle is −5m/s.
---
x(t)=2−5t+6t2
v(t)=dxdt
v(t)=ddt(2−5t+6t2)
- The derivative of a constant (2) is 0.
- The derivative of −5t is −5.
- The derivative of 6t2 is 12t (using the power rule).
v(t)=0−5+12t=−5+12t
v(0)=−5+12(0)=−5
v(0)=−5m/s
The initial velocity of the particle is −5m/s.
Topper's Solved these Questions
- MOTION IN ONE DIMENSIONBook:ERRORLESS Chapter:MOTION IN ONE DIMENSIONExercise:Relative Motion
Explore 13 Videos
- MOTION IN ONE DIMENSIONBook:ERRORLESS Chapter:MOTION IN ONE DIMENSIONExercise:Motion Under Gravity
Explore 81 Videos
- MOTION IN ONE DIMENSIONBook:ERRORLESS Chapter:MOTION IN ONE DIMENSIONExercise:Uniform Motion
Explore 24 Videos
- GRAVITATIONBook:ERRORLESS Chapter:GRAVITATIONExercise:SET
Explore 27 Videos
- MOTION IN TWO DIMENSIONBook:ERRORLESS Chapter:MOTION IN TWO DIMENSIONExercise:Exercise
Explore 319 Videos
Similar Questions
A particle moves along the X-axis. Its X-coordinate varies with time according to the expression x=4t+2r2, where x is in meters and t is in seconds. The position-time graph for this motion is shown in the figures previously. Note that the particle moves in the negative X-direction for the first second of motion, is at rest at the moment t=1s, and then heads back in the positive X-direction for t>1s.
Find the instantaneous velocity of the particle at t=2.5s.
View SolutionA particle moves along the X-axis. Its X-coordinate varies with time according to the expression x=4t+2r2, where x is in meters and t is in seconds. The position-time graph for this motion is shown in the figures previously. Note that the particle moves in the negative X-direction for the first second of motion, is at rest at the moment t=1s, and then heads back in the positive X-direction for t>1s.
Find the displacement of the particle in the time interval t=1sto t=3s.
View Solution
Knowledge Check
A particle moves along x-axis in such a way that its x-coordinate varies with time t according to the equation x=(8−4t+6t2) metre.
The velocity of the particle will vary with time according to the graph :-A B
B C
C D
D
A particle moves along x-axis in such a way that its r-coordinate varies with time't according to the equation x= (8−4t+6t2) metre. The velocity of the particle will vary with time according to the graph
A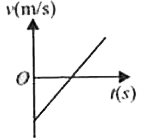 B
B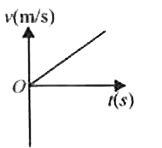 C
C D
D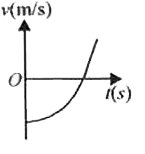
A particle moves along x axis in such a way that its coordinate x varies with time t according to the equation x=A0−A1t+A2t2. The initial velocity of the particle is.
AA0BA1CA2D−A1
A particle moves along x - axis in such a way that its x - co - ordinate varies with time according to the equation x=4−2t+t2. The speed of the particle will vary with time as
View SolutionA particle moves along the x-axis in such a way that its x-co-ordinate varies with time as x=2–5t+6t2.
The initial velocity and acceleration of particle will respectively be-
View SolutionA particle moves along the x-axis such that its co-ordinate (x) varies with time (t), according to the expression x=2−5t+6t2, where x is in metres and t is in seconds. The initial velocity of the particle is :–
View SolutionA particle moves in an XY-plane in such a way that its x and y-coordinates vary with time according to
x(t)=t3−32t,y(t)=5t2+12
Find the acceleration of the particle, if t = 3 s.
View SolutionA particle moves a distance x in time t according to equation x2=1+t2 . The acceleration of the particle is
View Solution

