Let $x_{0}, y_{0}$ be fixed real numbers such that $x_{0}^{2} + y_{0}^{2} > 1$ . If x, y are arbitrary real numbers such that $x^{2} + y^{2} \leq 1$ , then the minimum value of ${(x - x_{0})}_{0}^{2} + {(y - y_{0})}_{0}^{2}$ is

A

${(\sqrt{x_{0}^{2}} + (y_{0}^{2}) - 1)}^{2}$

B

$x_{0}^{2} + y_{0}^{2} - 1$

C

${(| X_{0} | + | Y_{0} | - 1)}^{2}$

D

${(| X_{0} | + | Y_{0} |)}^{2} - 1$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

$x_{0}^{2} + y_{0}^{2} > 1 x_{0} - y_{0} fixed$
$x, y a r i b i t a r y$
$x^{2} + y^{2} l i 1, Let x = cos θ$
$y = sin θ$
for men
$z = {(x - x_{0})}_{0}^{2} + {(y - y_{0})}_{0}^{2}$
$z = x^{2} + x_{0}^{2} + y^{2} + y_{0}^{2} - 2 (x x_{0} + y y_{0})$
$Put x - cos θ, y = sin θ$
$z = x_{0}^{2} + y_{0}^{2} - 2 (x_{0} cos θ + y_{0} sin θ)$
$\frac{d z}{d t h η} \Rightarrow 0 - 2 (- x_{0} sin θ + y_{0} cos θ)$
$\frac{d z}{d t h η} = 0$
$- x_{0} sin θ = - y_{0} cos θ$

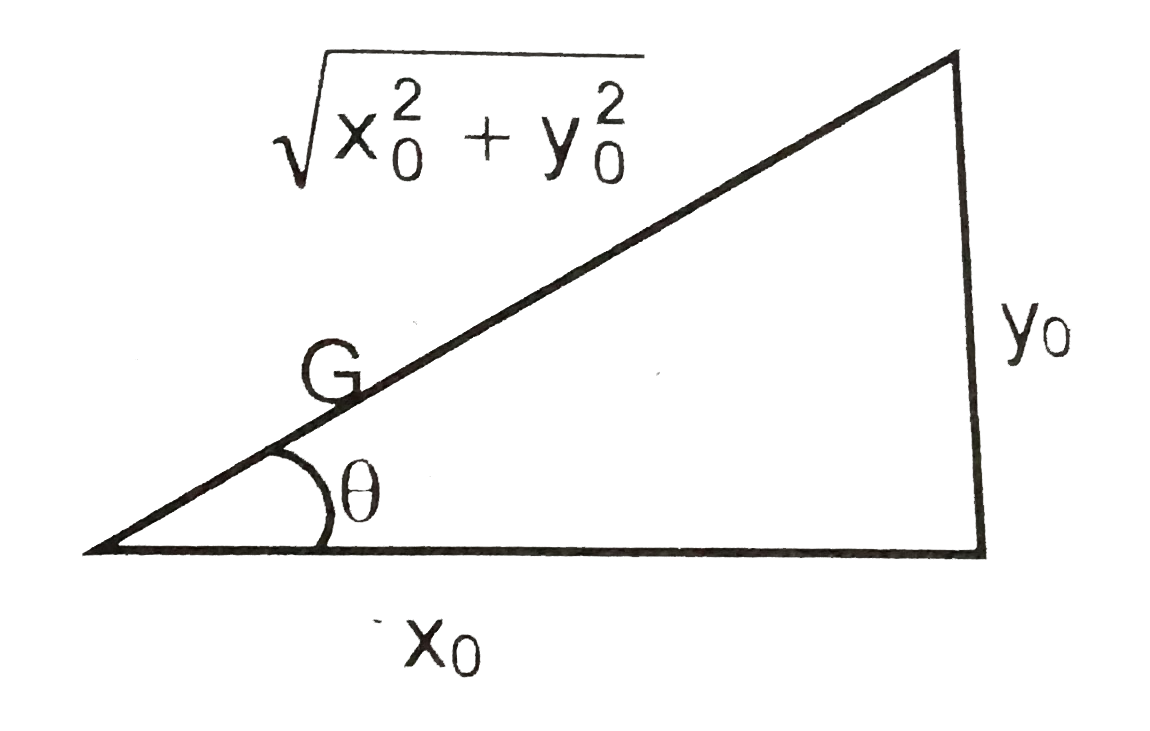
$tan θ = \frac{y_{0}}{x_{0}}$
$sin θ = \frac{y_{0}}{\sqrt{x_{0}^{2} + y_{0}^{2}}}$
$cos θ \frac{x_{0}}{\sqrt{x_{0}^{2} + y_{0}^{2}}}$
$x = \frac{x_{0}}{\sqrt{x_{0}^{2} + y_{0}^{2}}}, y = \frac{y_{0}}{\sqrt{x_{0}^{2} + y_{0}^{2}}}$
$z = {⎛ ⎜ ⎜ ⎝ \frac{x_{0}}{\sqrt{x_{0}^{2} + y_{0}^{2}}} - x_{0} ⎞ ⎟ ⎟ ⎠}_{0}^{2} + {⎛ ⎜ ⎜ ⎝ \frac{y_{0}}{\sqrt{x_{0}^{2} + y_{0}^{2}}} - y_{0} ⎞ ⎟ ⎟ ⎠}_{0}^{2}$
$x_{0} 2 {⎛ ⎜ ⎜ ⎝ \frac{1}{\sqrt{x_{0}^{2} + y_{0}^{2}}} - 1 ⎞ ⎟ ⎟ ⎠}^{2} + y_{0} 2 {⎛ ⎜ ⎜ ⎝ \frac{1}{\sqrt{x_{0}^{2} + y_{0}^{2}}} - 1 ⎞ ⎟ ⎟ ⎠}^{2}$
$(x_{0}^{2} + y_{0}^{2}) \frac{(1 - \sqrt{x_{0}^{2} + y_{0}^{2}})}{{(\sqrt{x_{0}^{2} + y_{0}^{2}})}^{2}}$
${(1 - \sqrt{x_{0}^{2} + y_{0}^{2}})}^{2} \Rightarrow {(\sqrt{x_{0}^{2} + y_{0}^{2}} - 1)}^{2}$

Updated on:21/07/2023

|

Class 12 MATHS QUESTION BANK

Topper's Solved these Questions

Similar Questions

Knowledge Check

Suppose x and y are real numbers and that $x^{2} + 9 y^{2} - 4 x + 6 y + 4 = 0$ , then the minimum value of $(4 x - 9 y)$ is
A1
B4
C5
D6
If real numbers x and y satisfy $x^{2} + y^{2} - 16 x + 30 y + 280 = 0$ then maximum value of ${(x^{2} + y^{2})}^{\frac{1}{2}}$ is
A15
B20
C25
D30
If $g (x) = max (y^{2} - x y) (0 \leq y \leq 1)$ , then the minimum value of g(x) (for real x) is
A $\frac{1}{4}$
B $3 - \sqrt{3}$
C $3 + \sqrt{8}$
D $\frac{1}{2}$

KVPY PREVIOUS YEAR-KVPY-Part 1 Mathematics

Home
Ask Doubt
Profile