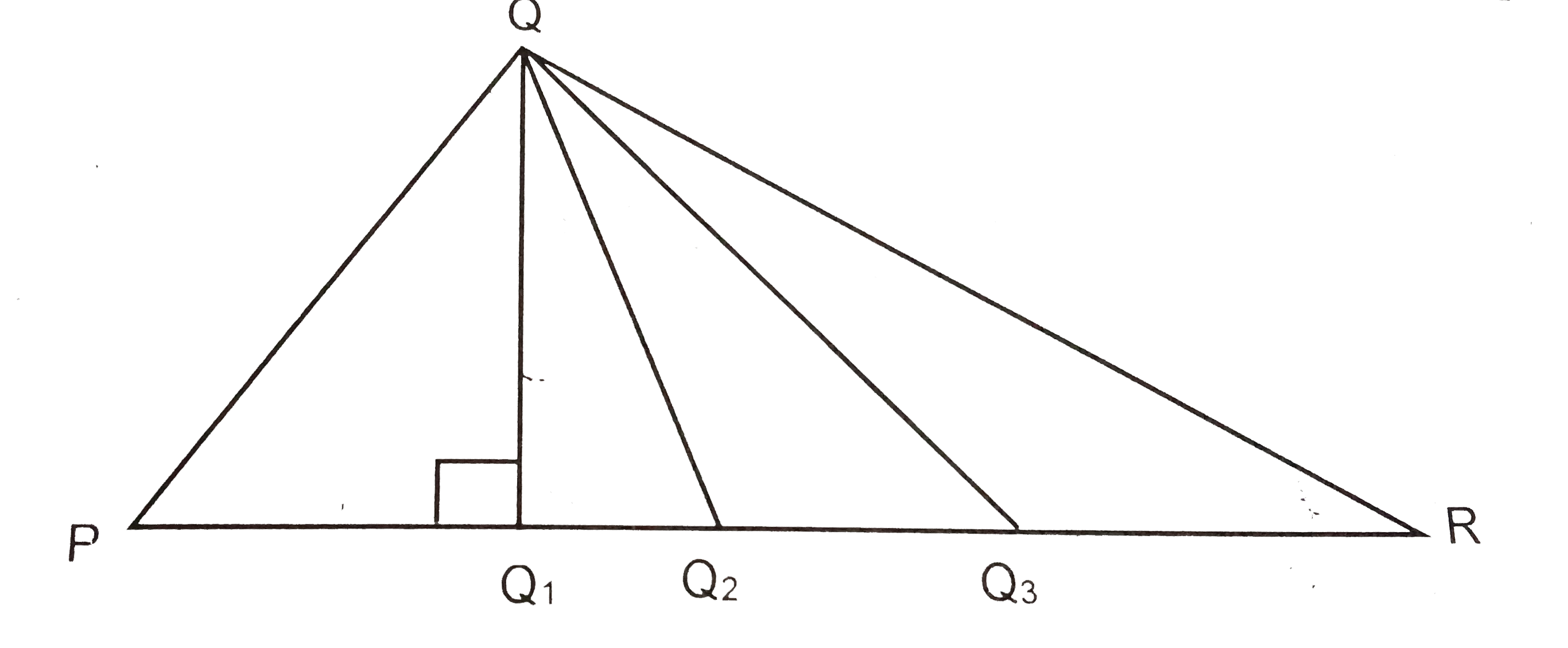
Let PQR be am acute-angled triangle in which PQ lt QR. From the vertex Q draw altitude $Q_{1}$ , the angle bisector $Q Q_{2}$ and the median $Q Q_{3} With Q_{1}, Q_{2}, Q_{3}$ lying on PR. Then

$P Q_{1} < P Q_{2} < P Q_{3}$

$P Q_{2} < P Q_{1} < P Q_{3}$

$P Q_{1} < P Q_{3} < P Q_{2}$

$P Q_{3} < P Q_{1} < P Q_{2}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

Updated on:21/07/2023

PQR is a right angled triangle at Q in which PQ = QR. If the hypotenuse of the triangle is 20 cm, then what is the area $(in c m^{2})$ of the triangle PQR ?
A $100 \sqrt{2}$
B100
C $50 \sqrt{2}$
D50
In, the charges on $C_{1}, C_{2}$ , and $C_{3}$ , are $Q_{1}, Q_{2}$ , and $Q_{3}$ , respectively.
.
A $Q_{2} = 8 μ C$
B $Q_{3} = 12 μ C$
C $Q_{1} = 20 μ C$
D $Q_{2} = 12 μ C$
$Δ P Q R$ is an isosceles triangle with $P Q = P R$ . If $∠ Q = 70^{\circ}$ , then find the other angles of the triangle.
A $30^{\circ}, 70^{\circ}$
B $40^{\circ}, 70^{\circ}$
C $70^{\circ}, 80^{\circ}$
D $50^{\circ}, 40^{\circ}$