Find the coordinates of one vertex of an equilateral triangle with centroid at the origin and the opposite side x+y−2=0.

A

(−1,−1)

B

(2,2)

C

(−2,−2)

D

(2,−2)

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

The correct Answer is:C

Let ABC be the equilateral triangle iwth vertex A(h,k).
Let the coordinates of D are (α,β).
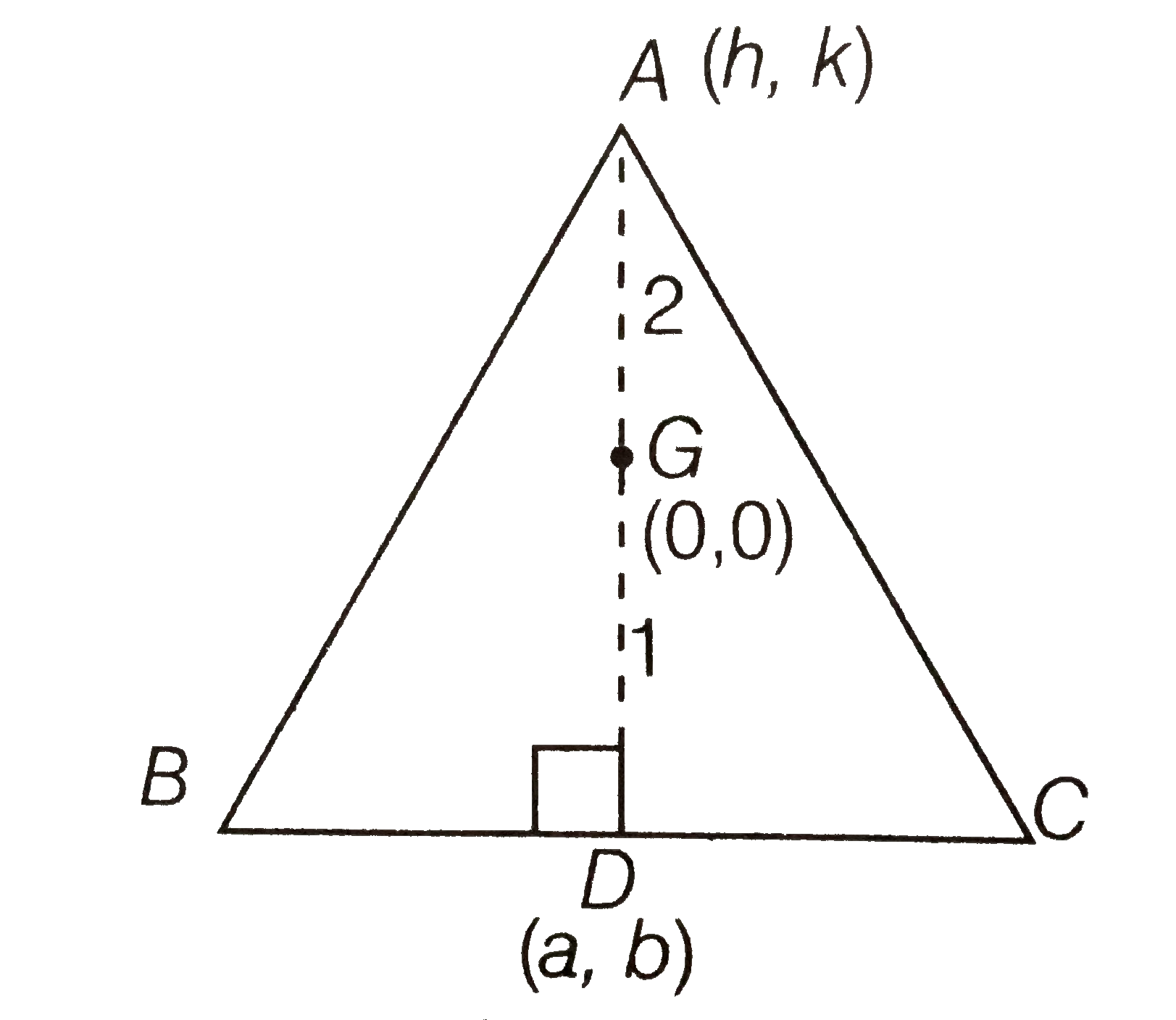
ocr_image
We know that 2:1 from the vertexA.
∴0=2α+h3 and 0=2β+k3
⇒2α=−h ......(i)
and 2β=−k
Also, D (α,β)lies on the line x+Y−2=0......(ii) .
∴α+β−2=0
AD⊥BC
Since, the slope of line BC i.e., mBC=−1
and slope of the line AG i.e., mAG=k−0h−0=kh
⇒(−1).(kh)=−1
⇒h=k ......(iii)
From Eqs. (i) and (iii),
2α=−h and 2β=−h
∴α=β
From Eq. (ii), 2α−2=0⇒α=1
If α=1 then β=1
So, the vertex A is (−2,−2).

Updated on:21/07/2023
|
Class 11MATHSSTRAIGHT LINES

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • One vertex of the equilateral triangle with centroid at the origin and one side as x+y−2=0 is

    A(-1,-1)
    B(2,2)
    C(-2,2)
    DNone of these

  • ABC is an equilateral triangle whose centroid is origin and base BC is along the line 11x+60y=122. Then

    AArea of the triangle is numerically equal to the perimeter
    BArea of triangle is numerically double the perimeter
    CArea of triangle is numerically three times the perimeter
    DArea of triangle is numerically half of the perimeter

  • If y=ax is one of the lines belonging to the family of lines representing the sides of an equilateral triangle with one vertex at the origin, then the product of the slopes of all the lines of this family is

    Aa3
    Ba(a2−3)
    Ca(1−3a2)
    Da(a2−3)1−3a2