The equation of the base of an equilateral triangle is $x + y = 2$ and its vertex is $(2, - 1) .$ Find the length and equations of its sides.

Video Solution

Text Solution

Verified by Experts

The correct Answer is:N/a

Given that, equilateral $Δ A B C$ having equation of base is $x + y = 2$ .
In $Δ A B D, {sin 60}^{\circ} = \frac{A D}{A B}$
$\Rightarrow A D = A B {sin 60}^{\circ} = A B \frac{\sqrt{3}}{2}$
$∵ A D = A B \frac{\sqrt{3}}{2}$ ......(i)
Now the length of perpendicular from $(2, - 1)$ to the line $x + y = 2$ is given by $A D = ∣ ∣ ∣ ∣ \frac{2 + (- 1) - 2}{\sqrt{1^{2} + 1^{2}}} ∣ ∣ ∣ ∣ = \frac{1}{\sqrt{2}}$
From Eq.(i) , $\frac{1}{\sqrt{2}} = A B \frac{\sqrt{3}}{2} A B = \sqrt{\frac{2}{3}}$

Updated on:21/07/2023

|

Class 11 MATHS STRAIGHT LINES

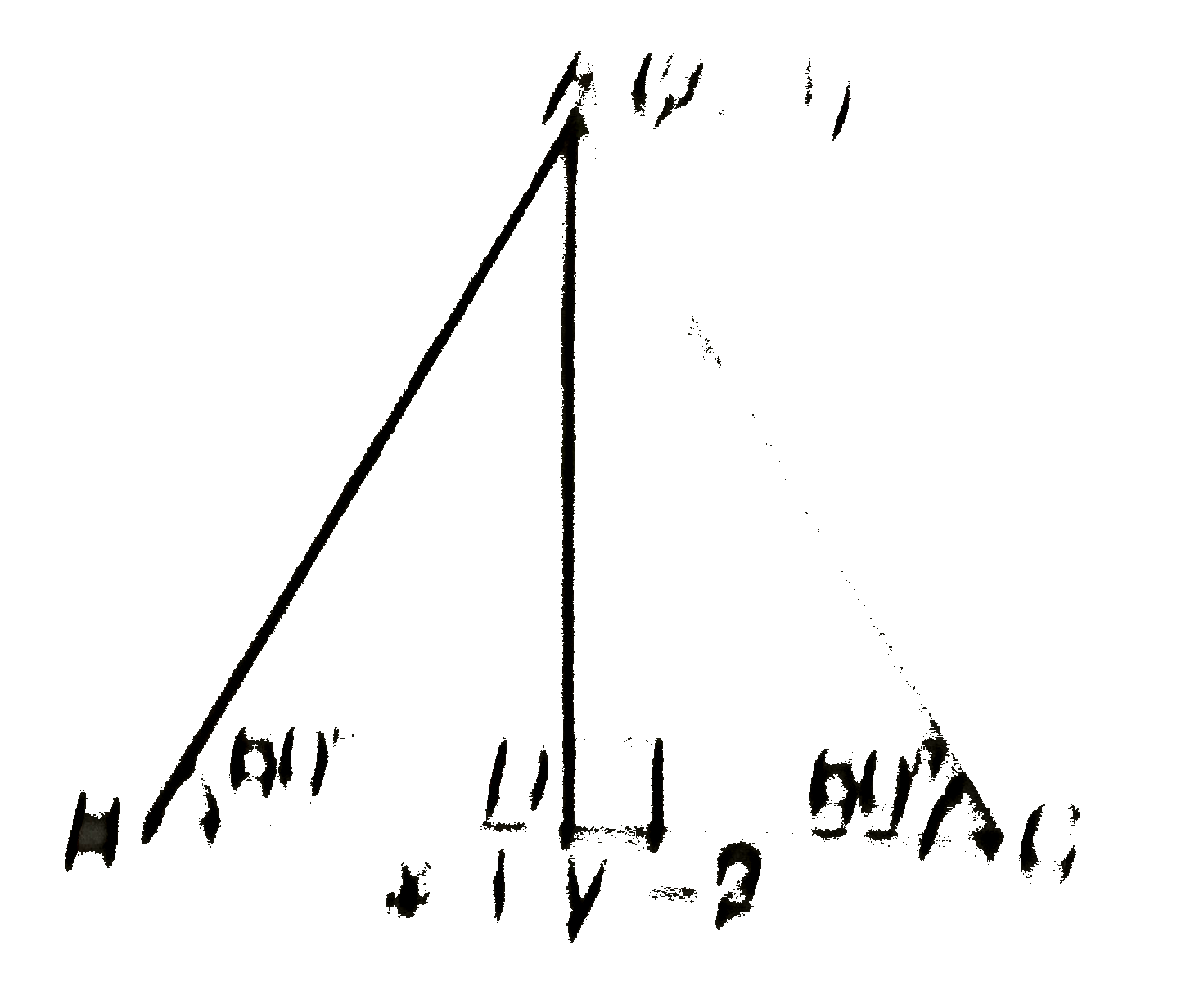
Topper's Solved these Questions

Similar Questions

Knowledge Check

If the equation of the base of an equilateral triangle is x + y = 2 and the vertex is (2, -1), then the length of the side of the triangle is (in unit)
A $\sqrt{\frac{2}{3}}$
B $\sqrt{\frac{3}{2}}$
C $\sqrt{\frac{1}{2}}$
D $\sqrt{\frac{5}{6}}$

NCERT EXEMPLAR-STRAIGHT LINES-Long Answer type

Home
Ask Doubt
Profile