The equation of the straight line which passes through the point (−4,3) such that the portion of the line between the axes is divided internally be the point in the ratio 5:3 is (a) 9x−20y+96=0 (b) 9x+20y=24 (c) 20x−9y+53=0 (d) none of these
The correct Answer is:N/a
Since, the line intersects X and Y -axes respectively at A(x,0)and B (0,y).
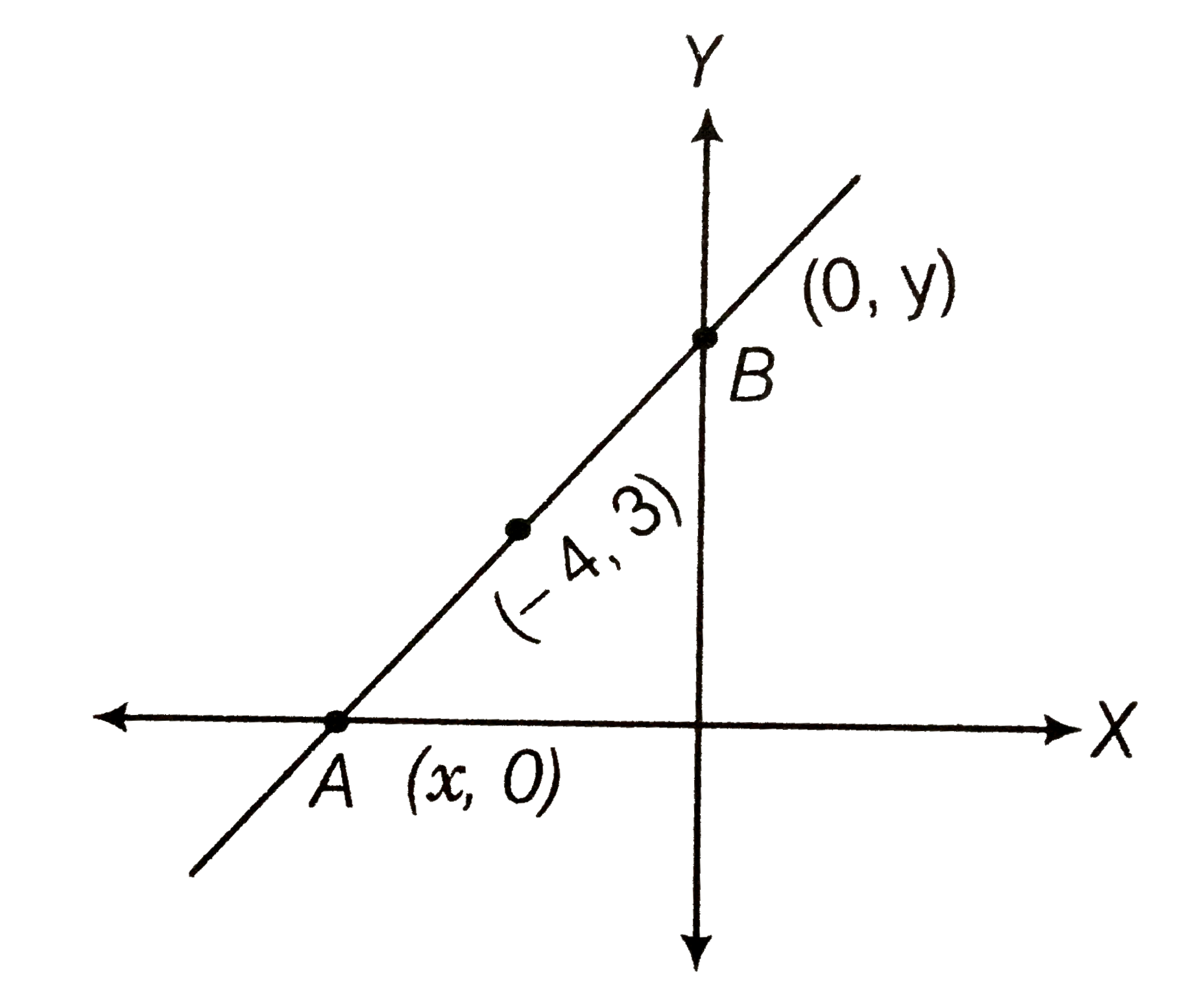
4=5×0+3x5+3
⇒−4=3x8⇒x=−323
and 3=5.y+3.05+3
⇒3=5y8⇒y=245
Since, the intercept on the Xand Y-axes respectively are a =−323 and b=245
∴ Equation of required line is x−32/3+y24/5=1
⇒−3x32+5y24=1
⇒−9x+20y=96
⇒9x−20y+96=0
Topper's Solved these Questions
- STRAIGHT LINESBOOK - NCERT EXEMPLARCHAPTER - STRAIGHT LINESEXERCISE - Objective type questions
20 Videos
- STRAIGHT LINESBOOK - NCERT EXEMPLARCHAPTER - STRAIGHT LINESEXERCISE - Fillers
6 Videos
- STRAIGHT LINESBOOK - NCERT EXEMPLARCHAPTER - STRAIGHT LINESEXERCISE - MATCHING THE COLUMN
3 Videos
- STATISTICSBOOK - NCERT EXEMPLARCHAPTER - STATISTICSEXERCISE - FILLERS
7 Videos
- TRIGONOMETRIC FUNCTIONS BOOK - NCERT EXEMPLARCHAPTER - TRIGONOMETRIC FUNCTIONS EXERCISE - TRUE/FALSE
9 Videos
Similar Questions
The equation of the straight line which passes through the point (−4,3) such that the portion of the line between the axes is divided internally be the point in the ratio 5:3 is (A) 9x-20y+96=0(B)9x+20y=24(C)20x+9y+53=0 (D) None of these
View SolutionThe equation of straight line which passes through the point (-4,3) such that the portion of the line between the axes is divided by the point in ratio 5:3 is -
View Solution
Knowledge Check
Equation of the line passing through the point (−4,3)and the portion of the line intercepted between the axes which is divided internally in the ratio 5:3 by this point, is
A9x+20y+96=0B20x+9y+96=0C9x−20y+96=0DNone of theseEquation of straight line passing through the points (2,0)and(0,−3) is
Ax2−y3=1By3−x2=1Cx3−y2=1Dy2−x3=1
Find the equation of the straight line that passes through the point A(−5,−4) and is such that the portion intercepted between the axes is divided by the point A in the ratio 1:2 (internally).
View SolutionThe equation of the straight line passing through the point (4,3) with slope 2 is 2x−y−5=0.
View SolutionA straight line passes through the point (1,2) and is such that the portion of it intercepted between the axes is divided internally at the point in the ratio 3:2. Find the equation of the line.
View SolutionA straight line passes through the point (-5,2) and the portion of the line intercepted between the axes is divided at this point in the ratio 2:3. Find the equation of the line.
View SolutionFind the equation of the straight line which passes through the point (2,−3) and the point intersection of the lines x+y+4=0and3x−y−8=0.
View SolutionFind the equation of the straight line passing through (3, 4) and the point of the intersection of the lines 5x−y=9 and x+6y=8
View Solution
