P1,P2 are points on either of the two lines y−√3|x|=2 at a distance of 5 units from the poinföf intersection. Find the coordinates of the foot of perpendiculars drawn from P1,P2 on the bisector the angle between the given lines.

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

The correct Answer is:N/a

Given equation of lines are y−√3x=2 [∵x≥0]
and y+√3x=2 [∵x≤0]
∵y=√3x+2 ......(i)
and y=−√3x+2 .....(ii)
⇒√3x+2=−√3x+2
⇒2√3x=0⇒x=0
On putting x=0in Eq. (i), we get
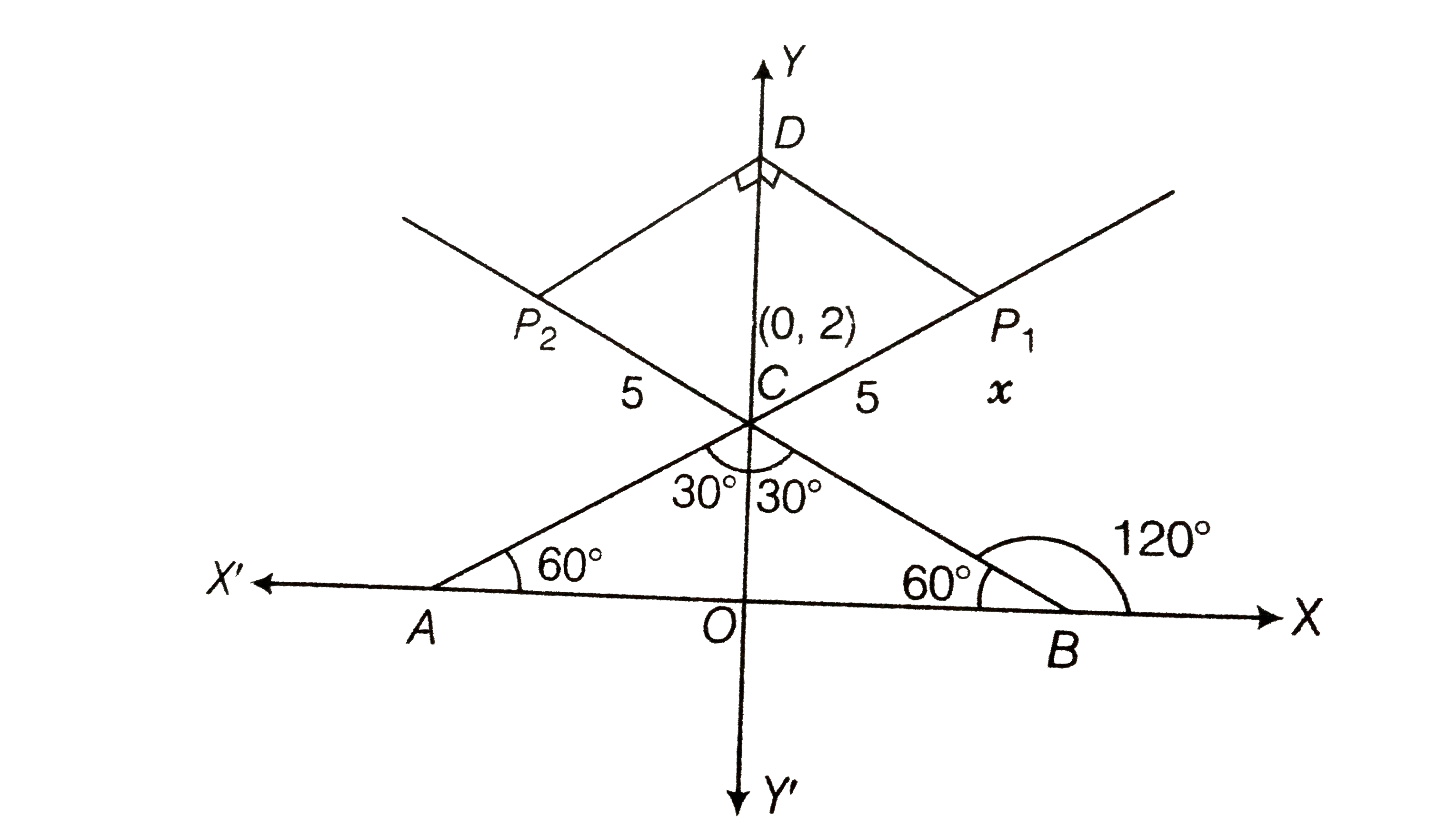
ocr_image
So, the point of intersection of line (i) and (ii) is (0,2).
Here, OC=2
In ΔDEC,CDCE=cos30∘
∴CD=5cos30∘=5.√32
⇒OD=OC+CD=2+5√32
So, the coordinate of the foot of perpendicular are (0,2+5√32)

Updated on:21/07/2023
|
Class 11MATHSSTRAIGHT LINES

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • P is a point on either of the two lines y−√3|x|=2 at a distance 5 units from their point of intersection The coordinates of the foot of the perpendicular from P on the bisector of the angle between them are

    A{0,12(4+5√3)}
    B{(0,12(4−5√3)}
    C(52,5√32)
    DNone of these