Find the equations of the diagonals of the square formed by the lines x=o,y=0,x=1 and y=1.
y=x,y+x=1
y=x,x+y=2
2y=x,y+x=13
y≡2x,y+2x=1
The correct Answer is:A
Equation of OB is y−0=1−01−0(x−0)
y=x
and equation of AC is y−0=1−00−1(x−1)
y=x+1
⇒x+y−1=0
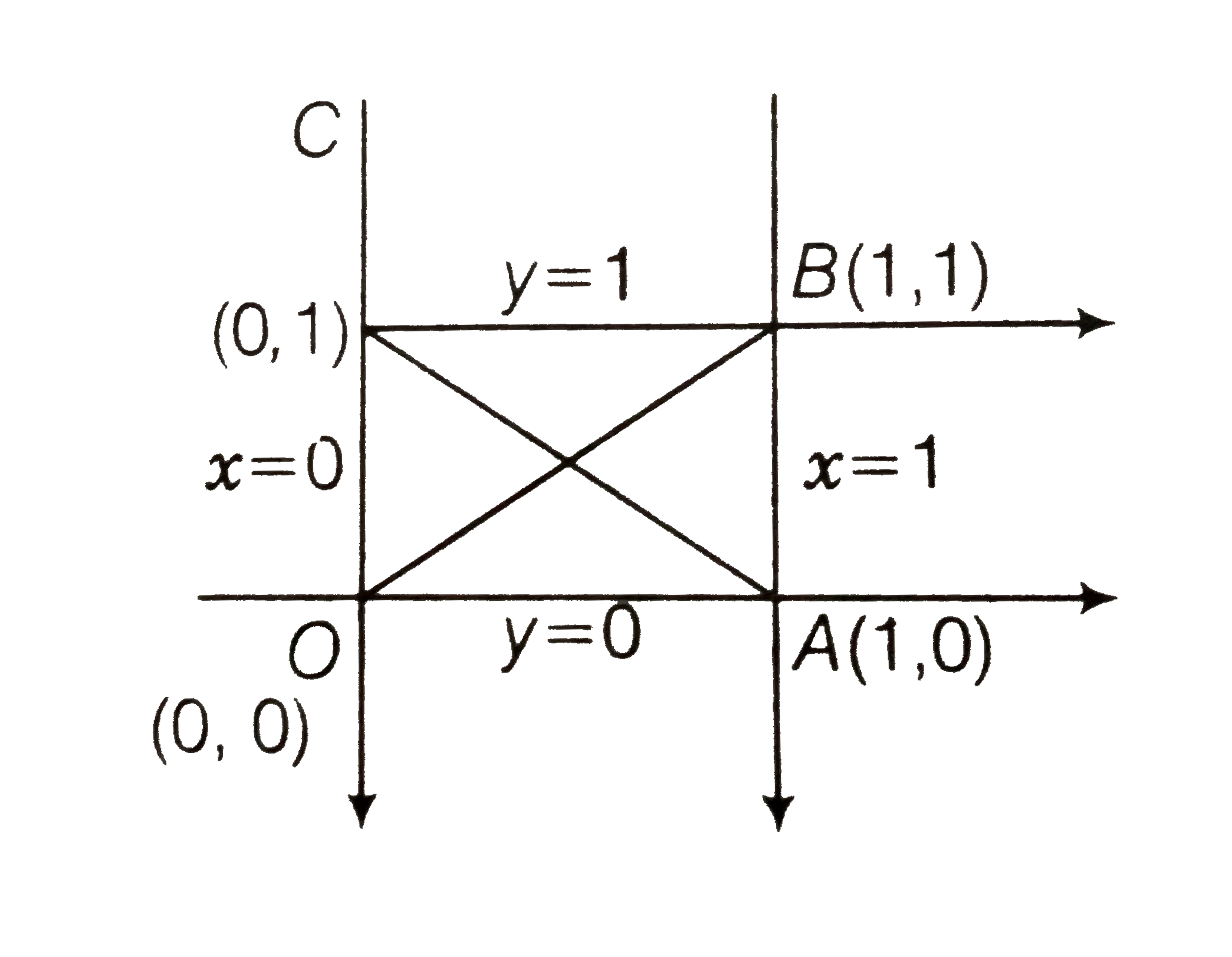
Topper's Solved these Questions
- STRAIGHT LINESBOOK - NCERT EXEMPLARCHAPTER - STRAIGHT LINESEXERCISE - Fillers
6 Videos
- STRAIGHT LINESBOOK - NCERT EXEMPLARCHAPTER - STRAIGHT LINESEXERCISE - TRUE/FALSE
9 Videos
- STRAIGHT LINESBOOK - NCERT EXEMPLARCHAPTER - STRAIGHT LINESEXERCISE - Long Answer type
9 Videos
- STATISTICSBOOK - NCERT EXEMPLARCHAPTER - STATISTICSEXERCISE - FILLERS
7 Videos
- TRIGONOMETRIC FUNCTIONS BOOK - NCERT EXEMPLARCHAPTER - TRIGONOMETRIC FUNCTIONS EXERCISE - TRUE/FALSE
9 Videos
Similar Questions
The equation of the diagonal through origin of the quadrilateral formed by the lines x=0,y=0,x+y−1=0 and 6x+y−3=0, is
View SolutionIf the equations of the diagonals of the parallelogram formed by the lines, 2x−y+7=0;2x−y−5=0;3x+2y−5=0and3x+2y+4=0 are ax+by−5=0andpx+qy+1=0. Find the value of (a+b+p+q).
View Solution
Knowledge Check
Joint equation of the diagonals of the square formed by the pairs of lines xy+4x−3y−12=0 and xy−3x+4y−12=0, is
Ax2−y2+x−y=0Bx2−y2+x+y=0Cx2+2xy+y2+x+y=0Dx2−2xy+y2+x−y=0The equation of the diagonal of the square formed by the pairs of lines xy+4x−3y−12=0 and xy−3x+4y−12=0 is
Ax−y=0Bx+y+1=0Cx+y=0Dx−y+1=0The equation of the diagonal through origin of the quadrilateral formed by the lines x=0,y=0,x+y−1=0 and 6x+y−3=0, is
A4x−3y=0B3x−2y=0Cx=yDx+y=0
Find the area of the triangle formed by the lines x=0, y=1 and 2x+y=2.
View SolutionThe equations of the diagonals of the square formed by the pairs of straight lines 3x2+8xy−3y2=0 and 3x2+8xy−3y2+2x−4y−1=0 are
View SolutionThe equation of the circumcircle of the triangle formed by the lines x=0,y=0,xa−yb=1, is
View SolutionFind the equation of the circle which circumscribes the triangle formed by the lines x=0, y=0 and lx+my=1.
View SolutionThe diagonal of the rectangle formed by the lines x2−7x+6=0 and y2−14y+40=0 is
View Solution