Using the conservation laws, demonstrate that the total mechanical energy of a planet of mass m moving around the Sun along an ellipse depends only on its semi-major axis a. Find this energy as a function of a.
−GMsm2a
GMsm2a
GMsm3a
−GMsm3a
The correct Answer is:A
Step by step video, text & image solution for Using the conservation laws, demonstrate that the total mechanical energy of a planet of mass m moving around the Sun along an ellipse depends only on its semi-major axis a. Find this energy as a function of a. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
If the angular momentum of a planet of mass m, moving around the Sun in a circular orbit is L, about the center of the Sun, its areal velocity is :
View SolutionThe total mechanical energy of a 2.00 kg particle moving along an x axis is 5.00 J. The potential energy is given as U(x)=(x4−2.00x2)J, with x in meters. Find the maximum velocity.
View Solution
Knowledge Check
A planet of mass m is moving around the sun in an elliptical orbit of semi-major axis a :
AThe total mechanical energy of the planet is varying periodically with timeBThe total energ of the planet is constant and equals −GmMs2a,Ns is mass of sunCTotal mechanical energy of the planet is constant and equals −GmMsa,M2 is mass of sunDDate is insufficient of arrice at a conclusionKepler's law starts that square of the time period of any planet moving around the sun in an elliptical orbit of semi-major axis (R) is directly proportional to
ARB1RCR3D1R3The satellite of mass m is orbiting around the earth in a circular orbit with a velocity v.What will be its total energy ?
A(3/4)mv2B(1/2)mv2Cmv2D(1/2)mv2
The motion of a planet around sun in an elliptical orbit is shown in the following figure. Sun is situated at one focus. The shaded areas are equal. If the planet takes time t1 and l2 in moving from A to B and from C to D respectively, then
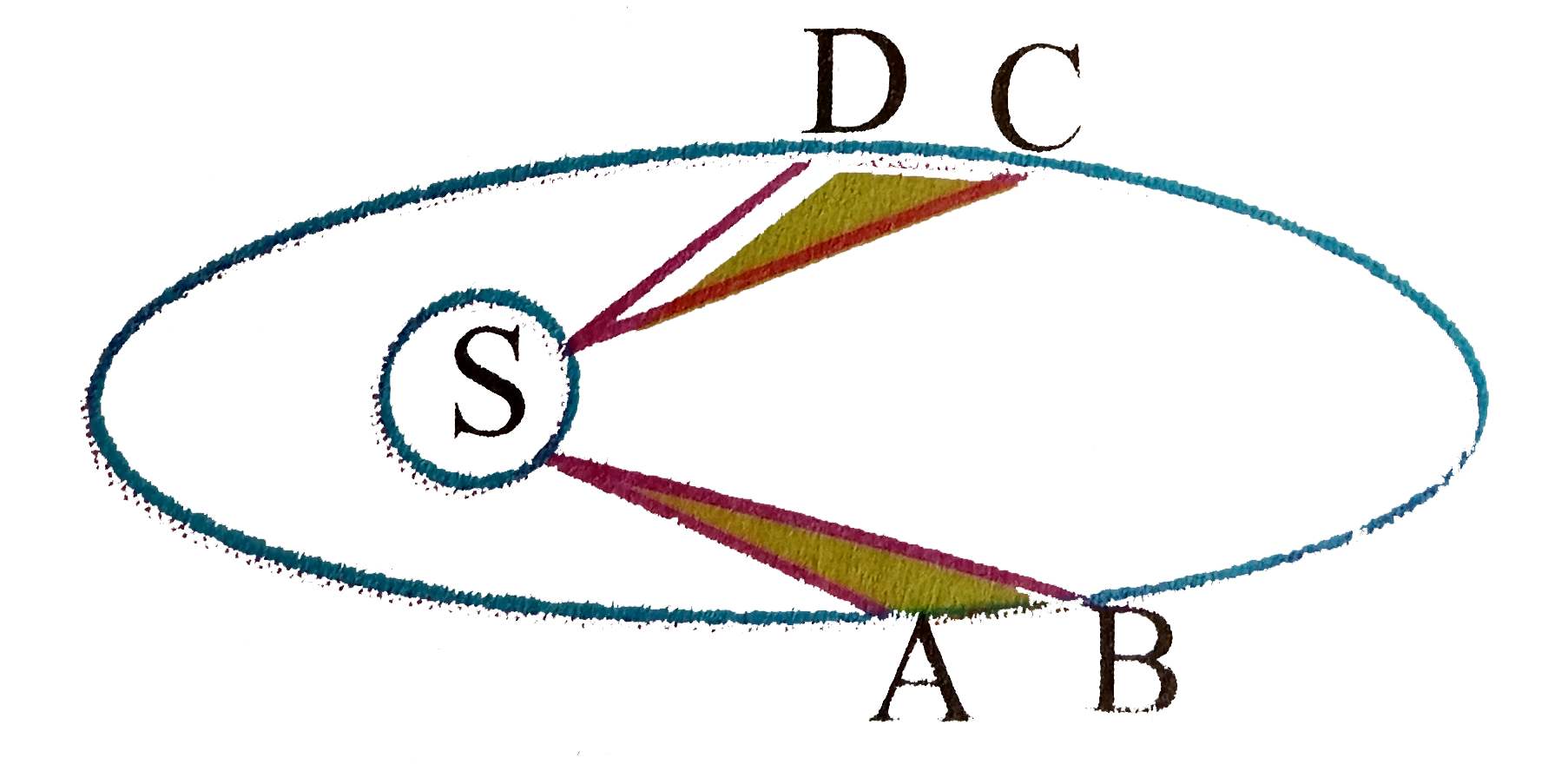
View SolutionThe motion of a planet around sun in an elliptical orbit is shown in the following figure. Sun is situated at one focus. The shaded areas are equal. If the planet takes time t1 and l2 in moving from A to B and from C to D respectively, then
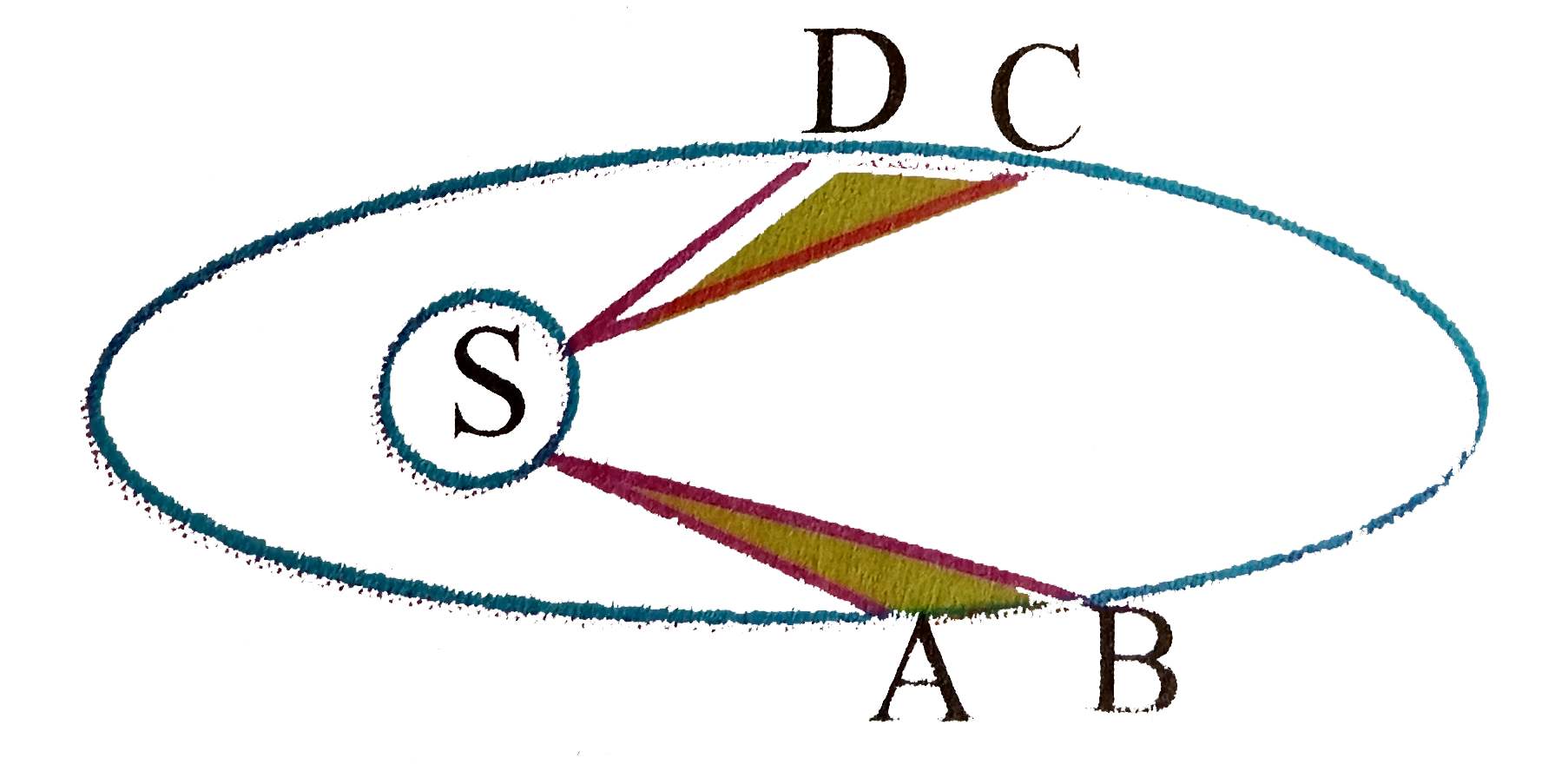
View Solution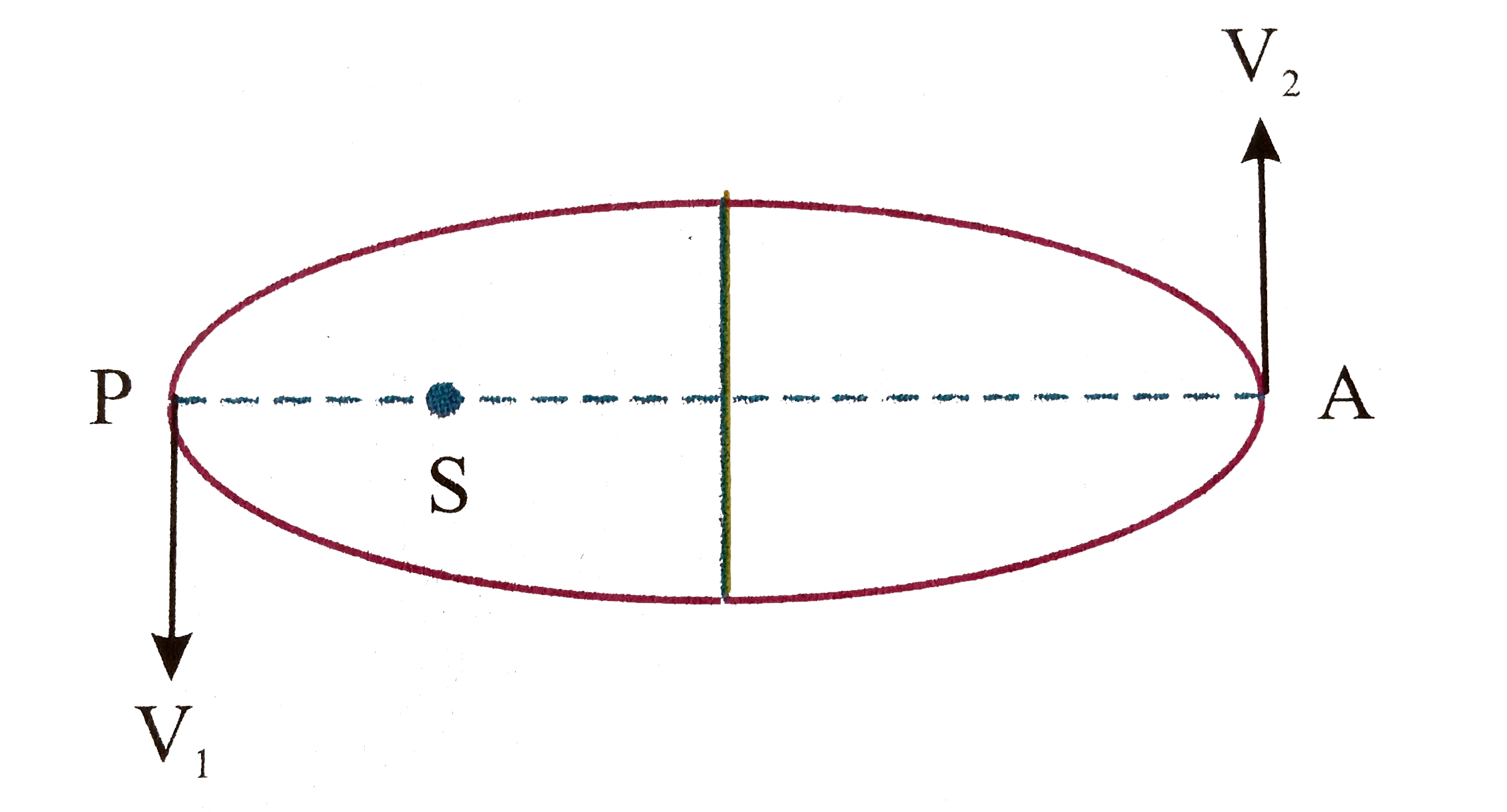
A planet of mass m is moving in an elliptical orbit around the sun of mass M. The semi major axis of its orbit is a, eccentricity is e.
Find total energy of planet interms of given parameters.
View SolutionAn artificial moving in a circular orbit around the earth has total mechanical energy E0. Its kinetic energy is
View SolutionThe variation of potential energy of a particle of mass m = 5kg to its x-coordinate . The particle moves under the effect of this conservative force only along the x-axis. Then, choose the correct option.
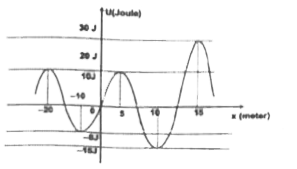
View Solution
