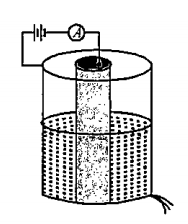
Two long coaxial cylindrical metal tubes (inner radius a, outer radius b) stand vertically in a tank of dielectric oil (of mass density ρ , dielectric constant K). The inner one is maintained at potential V and the outer one is grounded. To what equilibrium height (h) does the oil rise in the space between the tubes? [Assume this height ( h) as an equilibrium height]
ε02V2(K−1)gρ(b2−a2)1n(ba)
ε02V2(K−1)ρ(b2−a2)g1n(ba)
4ε02V2(K−1)gρ(b2−a2)1n(ba)
6ε02V2(K−1)ρ(b2−a2)g1n(ba)
The correct Answer is:B
To solve the problem of determining the equilibrium height h to which the dielectric oil rises in the space between two coaxial cylindrical tubes, we can follow these steps:
Step 1: Understand the System
We have two coaxial cylindrical tubes: the inner tube has a radius a and is maintained at a potential V, while the outer tube has a radius b and is grounded. The space between the tubes is filled with dielectric oil of density ρ and dielectric constant K.
Step 2: Model the Capacitor
The system can be modeled as a capacitor with two regions: one filled with air (or vacuum) and the other filled with dielectric oil. The capacitance C of the system can be expressed as:
C=Cair+Coil
where Cair and Coil are the capacitances of the air and oil regions, respectively.
Step 3: Calculate Capacitances
The capacitance of the air region (between the inner tube and the outer tube) can be given by:
Cair=2πϵ0Lln(b/a)
The capacitance of the oil region (which is filled with dielectric) can be expressed as:
Coil=2πKϵ0Lln(b/a)
Thus, the total capacitance becomes:
C=2πϵ0Lln(b/a)+2πKϵ0Lln(b/a)=2πϵ0L(1+K)ln(b/a)
Step 4: Energy Stored in the Capacitor
The energy E stored in the capacitor can be expressed as:
E=12CV2
Substituting for C:
E=12⋅2πϵ0L(1+K)ln(b/a)V2
Step 5: Force on the Oil
The force acting on the oil column due to the electric field can be derived from the energy stored in the capacitor. The force F can be expressed as:
F=dEdh
We can relate this to the weight of the oil column:
F=ρgVoil=ρgπ(b2−a2)h
where Voil is the volume of the oil column.
Step 6: Equate Forces
At equilibrium, the upward force due to the electric field must balance the downward gravitational force on the oil:
dEdh=ρgπ(b2−a2)h
Substituting for E and differentiating with respect to h gives us the equation to solve for h.
Step 7: Solve for h
After performing the necessary differentiation and rearranging, we can isolate h to find the equilibrium height:
h=V2(1+K)2ρgln(b/a)
Final Result
Thus, the equilibrium height h to which the oil rises in the space between the tubes is given by:
h=V2(1+K)2ρgln(b/a)
---
We have two coaxial cylindrical tubes: the inner tube has a radius a and is maintained at a potential V, while the outer tube has a radius b and is grounded. The space between the tubes is filled with dielectric oil of density ρ and dielectric constant K.
The system can be modeled as a capacitor with two regions: one filled with air (or vacuum) and the other filled with dielectric oil. The capacitance C of the system can be expressed as:
C=Cair+Coil
where Cair and Coil are the capacitances of the air and oil regions, respectively.
The capacitance of the air region (between the inner tube and the outer tube) can be given by:
Cair=2πϵ0Lln(b/a)
The capacitance of the oil region (which is filled with dielectric) can be expressed as:
Coil=2πKϵ0Lln(b/a)
Thus, the total capacitance becomes:
C=2πϵ0Lln(b/a)+2πKϵ0Lln(b/a)=2πϵ0L(1+K)ln(b/a)
The energy E stored in the capacitor can be expressed as:
E=12CV2
Substituting for C:
E=12⋅2πϵ0L(1+K)ln(b/a)V2
The force acting on the oil column due to the electric field can be derived from the energy stored in the capacitor. The force F can be expressed as:
F=dEdh
We can relate this to the weight of the oil column:
F=ρgVoil=ρgπ(b2−a2)h
where Voil is the volume of the oil column.
At equilibrium, the upward force due to the electric field must balance the downward gravitational force on the oil:
dEdh=ρgπ(b2−a2)h
Substituting for E and differentiating with respect to h gives us the equation to solve for h.
After performing the necessary differentiation and rearranging, we can isolate h to find the equilibrium height:
h=V2(1+K)2ρgln(b/a)
Thus, the equilibrium height h to which the oil rises in the space between the tubes is given by:
h=V2(1+K)2ρgln(b/a)
Topper's Solved these Questions
Similar Questions
Two long cylindrical metal tubes stand on insulating floor. A dielectric oil is filled between plates. Two tubes are maintained with potential difference v. A small hole is opened at bottom then
View SolutionWhen one end of a tube of radius r is immersed vertically in a liquid of density ρ, surface tension S, the rise of liquid in the tube is h and angle of contact is θ . If the tube is broken and its length is made h'(<h), then find the value of height of rise of liquid in the tube and angle of contact.
View Solution
Knowledge Check
Two long coaxial cylindrical metal tubes stand on an insulatiog floor as shown in figure. A dielectric oil is filled in the annular region between the tubes. The tubes are maintained at a constant potential difference V. A small hole is opened at bottom then :
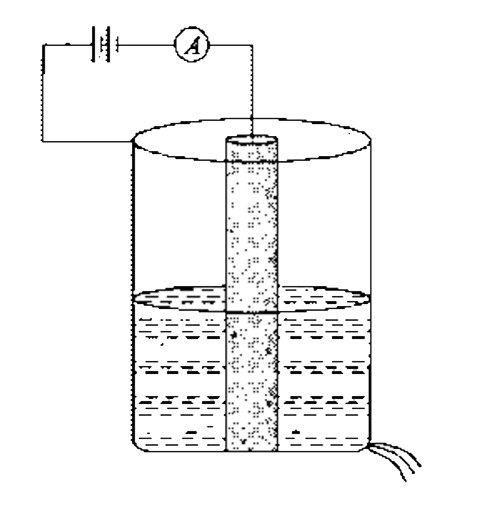 AReading of ammeter remain constantBCapacitance of system increasesCCurrent in circuit is dependent on area ofholeDCurrent in circuit is inversely proportional to dielectric constant
AReading of ammeter remain constantBCapacitance of system increasesCCurrent in circuit is dependent on area ofholeDCurrent in circuit is inversely proportional to dielectric constantTwo long coaxial and conducting cylinders of radius a and b are separated by a material of conductivity σ and a constant potential difference V is maintained between them, by a battery. Then the current, per unit length of the cylinder flowing from one cylinder to the other is
A4πσln(b/a)VB4πσ(b+a)VC2πσln(b/a)VD2πσ(b+a)VTwo long coaxial and conducting cylinders of radius a and b are separated by a material of conductivity σ and a constant potential difference V is maintained between them by a battery. Then the current per unit length of the cylinder flowing from one cylinder to the other is
A4πσln(b/a)VB4πσb/aVC2πσln(b/a)VD2πσb+aV
When a capillary tube of radius r is dipped vertically in a liquid of surface tension T, the liquid rises to a height h in the tube above the level outside the tube . If the angle of contact is θ the density of the liquid is ρ then the pressure difference between the points A and B is

View SolutionA coiaxial cable consists of two thin coaxial cylinders electrically connected at one end, an inner cylindrical conducting tube of radius a carrying a steady current l which is screened by an outer cylindrical conducting sheath of radius b which provides a return path. There is no dielectric medium present.
Use Ampere's theorem to derive the total magnetic energy stored in the space between the conductors, show that the inductance of a length l of the cable is
L=μ0l2πln(ba)
In this cable (a = 5 mm, b = 10 mm, l = 1000 m) is now employed in a (resistanceless) LC circuit containing a capacitance C = 1000 μF, determine the period of oscillations (neglect the capacitance of the cable itself).
View SolutionWhen a capillary tube of radius r is immersed in a liquid of density ρ, the liquid rises to a height h in it. If m is the mass of the liquid in the capillary tube, find the potential energy of this mass of the liquid in the tube.
View SolutionIn the last question let the length of the tube be L and its outer radius be R. Water rises in it to a height h. Calculate the vertical force needed to hold the tube in this position. Mass of empty tube is M.
View SolutionA railway track is banked for a speed v, by making the height of the outer rail h higher than that of the inner rail. If the distance between the rails is l and the radius of the curvature of the track is r, then
View Solution
