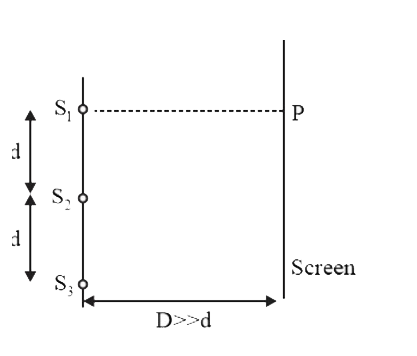
Consider the interference at P between waves emitting from three coher

Consider an interference pattern between two coherent sources. If $I_{1} and I_{2}$ be intensities at points where the phase difference are $\frac{π}{3} and \frac{2 π}{3}$ and respectively , then the intensity at maxima is
A $\frac{I_{2} - 3 I_{1}}{2}$
B $\frac{I_{1} - 3 I_{2}}{2}$
C $\frac{3 I_{2} - I_{1}}{2}$
D $\frac{3 I_{1} - I_{2}}{2}$
$S_{1} and S_{2}$ are two coherent sources. The intensity of both sources are same. If the intensity at the point of maxima is $4 W m^{- 2}$ , the intensity of each source is
A $1 W m^{- 2}$
B $2 W m^{- 2}$
C $3 W m^{- 2}$
D $4 W m^{- 2}$
Two coherent monochormatic light source are located at two vertices of an equilateral trangle. If the intensity due to each of the source independently is $1 W m^{- 2}$ at the third vertex. The resultant intensity due to both the sources at that point (i.e at the third vertex) is (in $W m^{- 2}$ )
Azero
B $\sqrt{2}$
C2
D4

The correct Answer is:36