Two sound waves each of wavelength λ and having the same amplitude A form two sources S1andS2 interfere at a point P. If the path difference S2P−S1P=λ3, then the amplitude of the resultant were at P will be
A
2A
A/2
3A/2
The correct Answer is:A
Path diff.= λ3
∴ Phase diff. =2πλ×λ3=2π3=120∘
Resultant amplitude
R=√A2+A2+2A2cos120∘
∴R=√2A2−2A2×12=A
Topper's Solved these Questions
- WAVE MOTIONBook:MARVEL PUBLICATIONChapter:WAVE MOTIONExercise:Test your grasp
Explore 15 Videos
- SURFACE TENSION Book:MARVEL PUBLICATIONChapter:SURFACE TENSION Exercise:MULTIPLE CHOICE QUESTIONS . (TEST YOUR GRASP )
Explore 10 Videos
- WAVE THEORY OF LIGHT AND POLARISATION Book:MARVEL PUBLICATIONChapter:WAVE THEORY OF LIGHT AND POLARISATION Exercise:TEST YOUR GRASP -10
Explore 15 Videos
Similar Questions
Two waves of the same frequency have amplitudes 1.60 and 2.20. They interfere at a point where their phase difference is 60.0∘. What is the resultant amplitude?
View SolutionIn Fig. , two point sources S1 and S2 which are in phase and separated by distance D=1.5λ , emit identical sound waves of wavelength λ.
(a) What is the path length difference of the waves from S1 and S2 at point P1, which lies on the perpendicular bisector of distance D, at a distance greater than D from the sources ? (That is, what is the difference in the distance from source S1 to point P1 and the distance from source S2 to P1?) What type of interference occurs at P1 ?
(b) What are the path length difference and type of interference at point P2 in fig.
(c ) Figure shows a circle with a radius much greater than D, centered on the midpoint between sources S1 and S2. What is the number of points N around this circle at which the interference is fully constructive? (That is, at how many points do the waves arrive exactly in phase?)
View Solution
Knowledge Check
Two waves of equal amplitude a from two coherent sources (S1&S2) interfere at a point R such that S2R−S1R=1.5λThe intensity at point R Would be
AZeroB2a2C5a2D6a2In the case of light waves from two coherent sources S1 and S2, there will be constructive interference at an arbitrary point P, the path difference S1P−S2P is
A(n+12)λBnλC(n−12)λDλ2_E01_054_Q01.png)
A monochromatic light source of wavelength λ is placed at S. three slits S1,S2 and S3 are equidistant from the source S and the point P on the screen S1P−S2P=λ/6 and S1P−S3P=2λ/3. if I be the intensity at P when only one slit is open the intensity at P when all the three slits are open is-A3IB5IC8IDzero
In a modified set up of Young's double slit experiment, it is given that SS2−SS1=λ4 i.e., the source S is not equidistant from the slits S1andS2.
(a) Obtain the condition for constructive and destructive interference at any point P on the screen in terms of the path difference Δ=S2P−S1P.
(b) Does the observed central bright fringe lie above or below O ? Give reason in support of your answer.
View SolutionTwo S.H.M.’s have zero phase difference and equal amplitudes A. The resultant amplitude on their composition will be
View SolutionAt two point P and Q on screen in Young's double slit experiment, waves from slits S1 and S2 have a path difference of 0 and λ4 respectively. The ratio of intensities at P and Q will be:
View SolutionAt two point P and Q on screen in Young's double slit experiment, waves from slits S1 and S2 have a path difference of 0 and λ4 respectively. The ratio of intensities at P and Q will be:
View Solution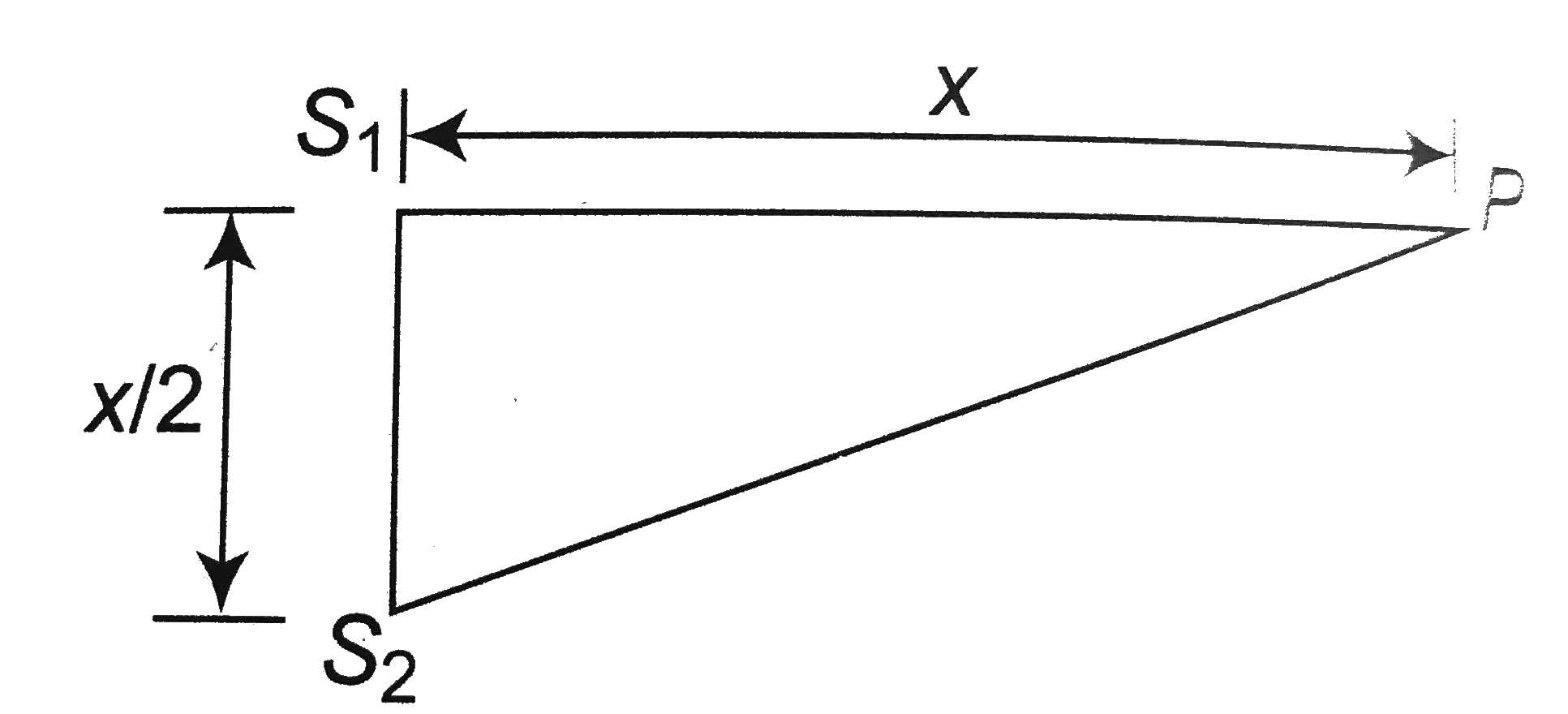
The wavelength of the waves arriving at P from two coherent sources S1 and S2 is 4m, while intensity of each wave is I0. The resultant intensity at P is 2I0. Find the minimum value of S2P
View Solution

