Consider an infinite long cylinderical conductor of radius R carrying a current I with a non uniform current density J=αr where a is a constant. Find the magnetic field for inside and outside prints.
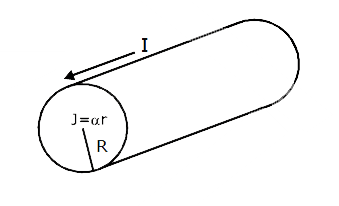
Inside αu03r2
Outside αu03Rr3
inside the outer conductor αμ03R2
Outside αμ03rR3
The correct Answer is:A, D
Step by step video, text & image solution for Consider an infinite long cylinderical conductor of radius R carrying a current I with a non uniform current density J=alphar where a is a constant. Find the magnetic field for inside and outside prints. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- MAGNETISM BOOK - MOTIONCHAPTER - MAGNETISM EXERCISE - EXERCISE-3 (Level-I)
46 Videos
- MAGNETISM BOOK - MOTIONCHAPTER - MAGNETISM EXERCISE - EXERCISE-3 (Level-II)
23 Videos
- MAGNETISM BOOK - MOTIONCHAPTER - MAGNETISM EXERCISE - EXERCISE-2 (Level-I)
40 Videos
- LOGIC GATESBOOK - MOTIONCHAPTER - LOGIC GATESEXERCISE - EXERCISE - 2
10 Videos
- MAGNETISM -1BOOK - MOTIONCHAPTER - MAGNETISM -1EXERCISE - Exercise - 3 SECTION -A
56 Videos
Similar Questions
A long cylindrical conductor of radius R carries a current i as shown in the figure. The current density J varies across the cross-section as J=kr2, where, k is a constant. Find an expression for the magnetic field B at a distance r(<R) from the axis

View SolutionA long cylidrical conductor of radius R carries a current i as shown in figure. The current desity J is a function of radius according to J=br, where b is a constant. Find an expression for the magnetic field B

a. at a distasnce r1<R and
b.at a distance r2>R, measured from the axis.
View Solution
Knowledge Check
An infinitely long cylinderical wire of radius R is carrying a current with current density j=αr3 (where α is constant and r is the distance from the axis of the wire). If the magnetic fixed at r=R2 is B1 and at r=2R is B2 then the ratio B2B1 is
A2B4C6D8A long cylindrical conductor of radius R carries I as shown. The current density is a function of radius r as j = br, where b is a constant. The magnetic field at a distance r1(r1<R) is
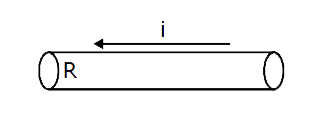 Aμ0br212Bμ0br312Cμ0br213Dzero
Aμ0br212Bμ0br312Cμ0br213DzeroThe figure shows the cross-section of a long conducting cylinder of inner radius a and outer radius b. The cylinder carries a current whose current density J=Cr2 where C is a constant. What is the magnitude of the magnetic field B at a point r, where a<r<b?
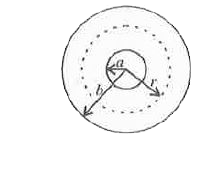 AB=μ0πC4πr2(r2−a2)BB=μ0πC4πr2(r4−a4)CB=μ0πC4π(r2−a2)DB=μ0πC4π(r4−a4)
AB=μ0πC4πr2(r2−a2)BB=μ0πC4πr2(r4−a4)CB=μ0πC4π(r2−a2)DB=μ0πC4π(r4−a4)
A long straight solid metal wire of radius R carries a current I, uniformly distributed over its circular cross-section. Find the magnetic field at a distance r from axis of wire (i) inside and (ii) outside the wire.
View SolutionA hollow cylindrical conductor of inner radius a and outer radius b carries a current I uniformly spread over its cross-section. Find the magnetic field induction at a point inside the body of the conductor at a distance r [where a<r<b] from the axis of the cylinder.
View SolutionA non-homogeneous cylinder of radius "R" carries a current I whose current density varies with the radial "distance "r" from the centre of the rod as J=σr where σ is a constant.The magnetic field at a point "P" at a distance r<R from the centre of the rod is
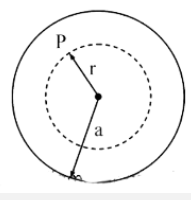
View SolutionThe figure shows the cross-section of a long cylindrical conductor of radius a carrying a uniformly distributed current i. The magnetic field due to current at P is :
View SolutionA cylindrical conductor of radius R carrying current i along the axis such that the magnetic field inside the conductor varies as B=B0r2(0<r≤R), then which of the following in incorrect?
View Solution
