The figure shows the cross-section of a long cylindrical conductor of radius a carrying a uniformly distributed current i. The magnetic field due to current at P is :
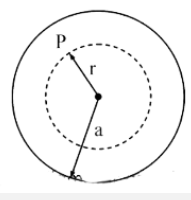
μir/(2πa2)
μ0ir2/(2πa)
μ0ia/(2πr2)
μ0ia2/(πr2)
The correct Answer is:A
B=μ0Ir2πR2 for 0<r<R for cylindrical conductor
Similar Questions
Figure shows a cross-section of a long ribbon of width ω that is carrying a uniformly distributed total current i into the page. Calculate the magnitude and direction of the magnetic field B at a point P in the plane of the ribbon at a distance d from its edge.

View SolutionA long thick conducting cylinder of radius 'R' carries a current uniformly distributed over its cross section :
View Solution
Knowledge Check
Figure shows the cross-sectional view of the hollow cylindrical conductor with inner radius 'R' and outer radius '2R', cylinder carrying uniformly distributed current along it's axis. The magnetic induction at point 'P' at a distance 3R2 from the axis of the cylinder will be
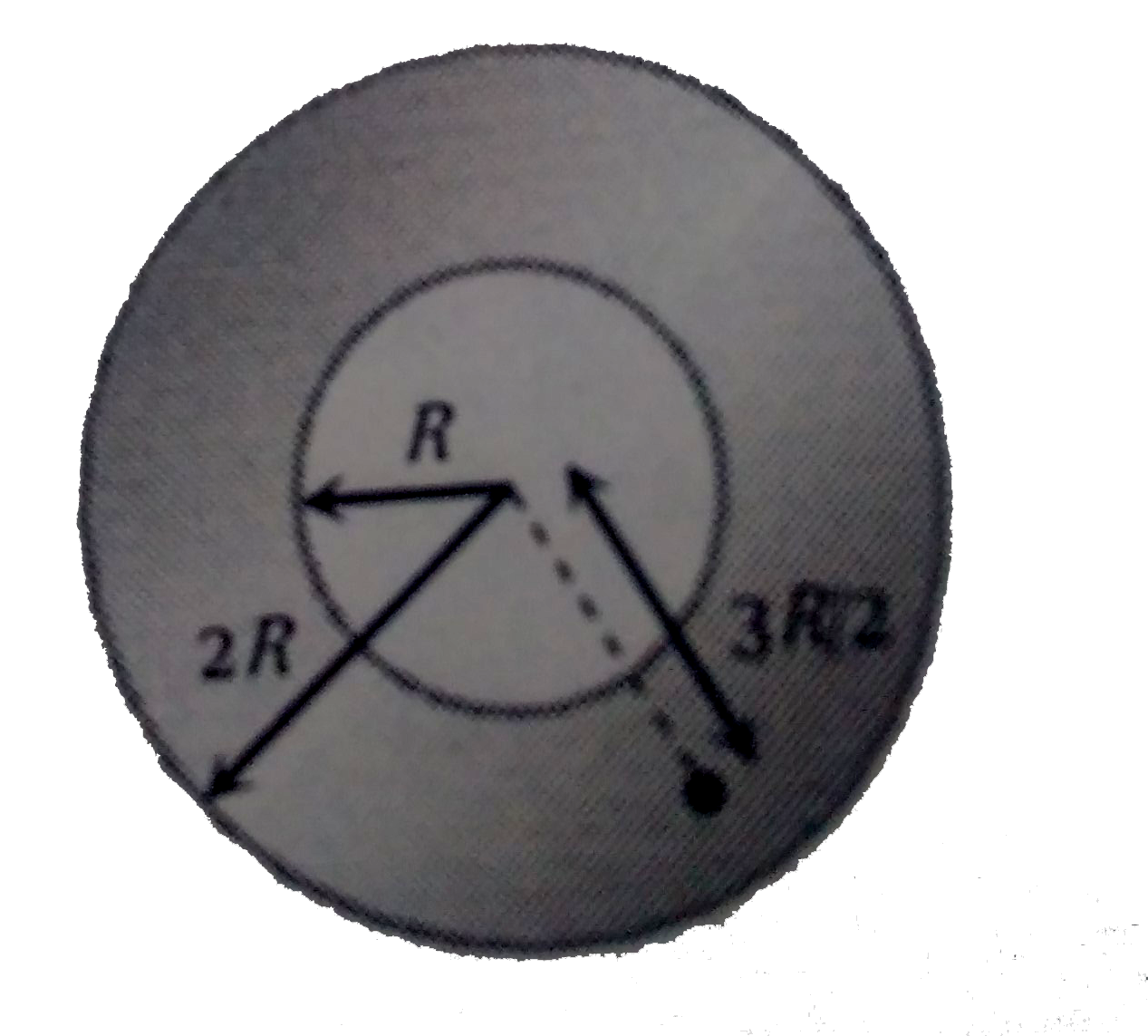 AZeroB5μ0i72πRC7μ0i18πRD5μ0i36πR
AZeroB5μ0i72πRC7μ0i18πRD5μ0i36πRAB and CD are long staright conductors, distance d apart, carrying a current I. The magnetic field on BC due to the currents in AB and CD
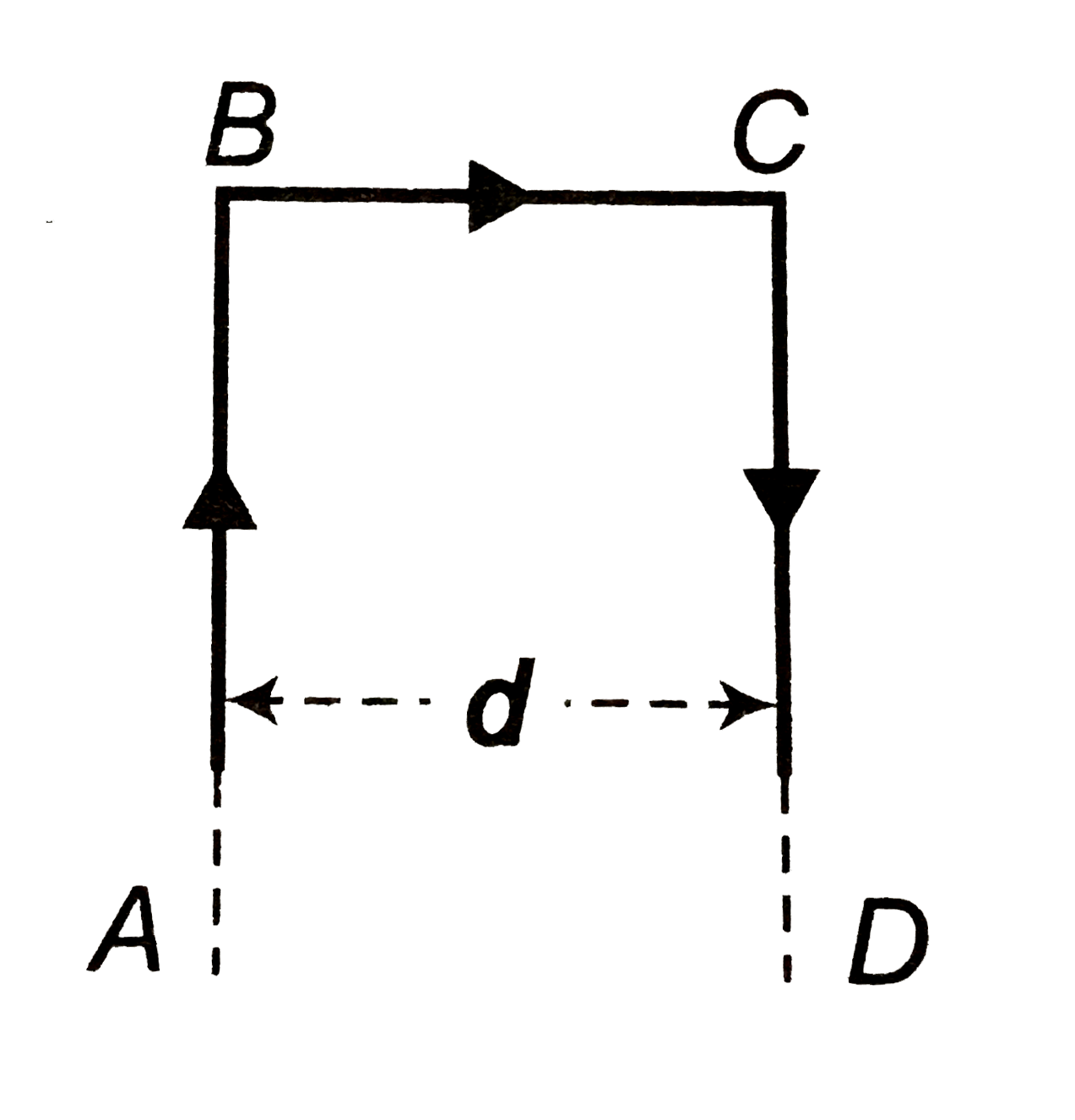 Ais zero at all pointsBis zero at this midpointChas different magnitudes at different pointsDis maximum at its midpoints
Ais zero at all pointsBis zero at this midpointChas different magnitudes at different pointsDis maximum at its midpointsCurrent flows through a straight cylindrical conductor of radius r. The current is distributed uniformly over its cross-section. The magnetic field at a distanace x from the axis of the conductor has magnitude B:
AB=0 at the axisBB∝x for 0≤x≤rCB∝1/x for x>rDB is maximum for x=r
Figure 29−64 shows a cross section of a long cylindrical conductor of radius a=4.00 cm containing a long cylindrical hole of radius b=1.50 cm. The central axes of the cylinder and hole are parallel and are distance d=2.00 cm apart, current i=5.25 A is uniformly distributed over the tinted area. (a) What is the magnitude of the magnetic field at the centre of the hole ? (b) Discuss the two special cases b=0 and d=0.
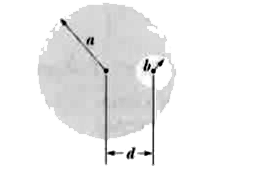
View SolutionMagnetic Field due to a Current Carrying Conductor
View SolutionA long straight solid conductor of radius 5(~cm) carries a current of 2 A waich is uniformly distributed over its circular cross-section. If the magnetic field induction at a distunce of 3 cm from the axis of the conductor is y×10−6T, then find the value of y.
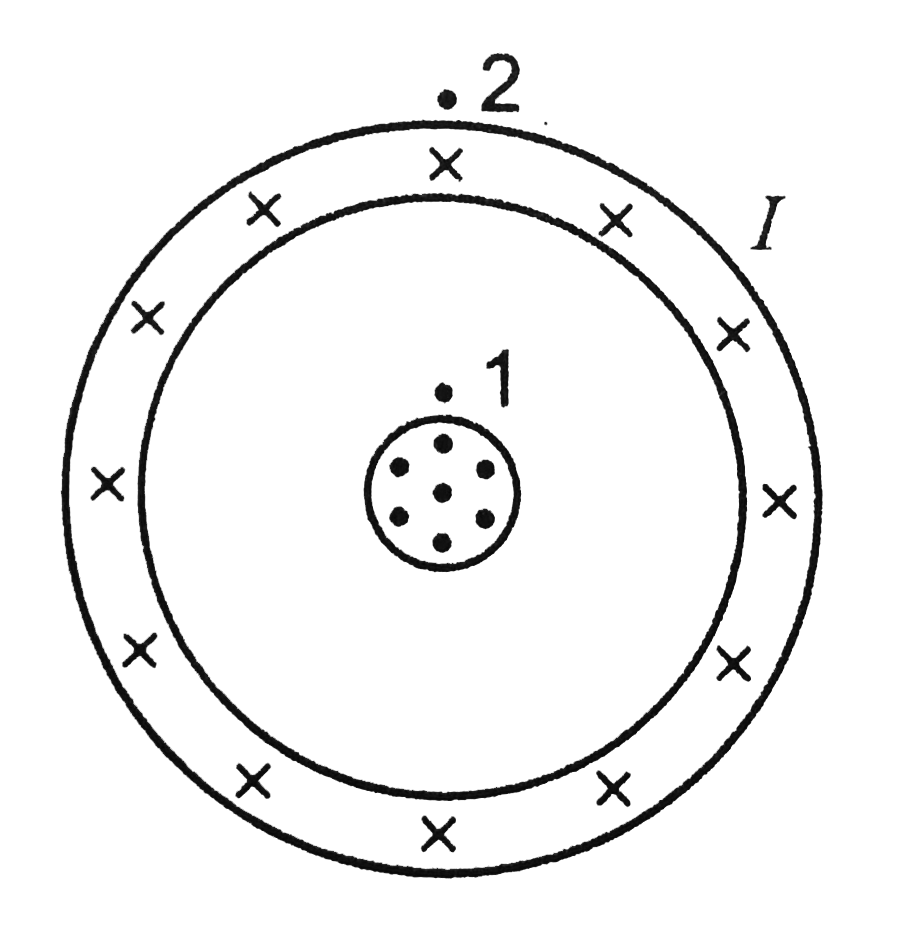
View SolutionThe figure shows the cross section of two long coaxial tubes carrying equal current I in opposites directions. If B1 and B2 are magnetic fields at point 1 and 2 as shown in figure then
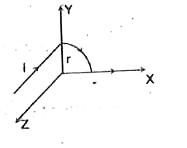
View SolutionShown in the figure is a conductor carrying a current i. the magnetic field at the origin is :
View Solution
