Figure shows a long straight wire of circular crosssection (radius a) carrying steady current I. The current I is uniformly distributed across this crosssection. Calculate the magnetic field in the region r<a and r>a.

(a)Consider the case r > a. The amperian loop, labelled 2, is a circle cocentric with the cross-section. For this loop,
L=2r
Ie = current enclosed by the loop = I
This result is the familiar exprssion for a long straight wire B(2πr)=μ0I
B=μ0I2πr
Bα1r(r > a)
(b) Consider the case r < a. The amperian loop is circle labelled 1. For this loop taking the radius of the circle to be r
L=2πr
Now the current enclosed Ie is not I, but is less than this value. Since the current distribution is uniform, the current enclosed is
Ie=I(πr2πa2)=Ir2a2
Using Ampere.s law, B(2πr)=μ0Ir2a2
B=(μ0I2πa2)r<>br>Bαr(r < a)
Figure show a plot of the magnitude of B with distance r from thạentre of the wure The direction of the field is tangential tothe respective circular loop (1 or 2) and given by the right hand rule described earlier in this section
Similar Questions
Figure shows a long straight wire of circular crosssection (radius a) carrying steady current I. The current I is uniformly distributed across this crosssection. Calculate the magnetic field in the region r<a and r>a.

View SolutionFigure shows a long straight wire of a circular cross-section (radius a) carrying steady current l. The current l is uniformly distributed across this cross-section. Calculate the magnetic field in the region r<aandr>a

View Solution
Knowledge Check
The figure shows a long striaght wire of a circular cross-section (radius a) carrying steady current I.The current I is unifromly distributed across this distance a/2 and 2a from axis is
A2:1B1:2C4:1D1:1A long straight wire of radius a carries a steady current i. The current is uniformly distributed across its cross section. The ratio of the magnetis field at (a)/(2)and(2a) is
A(1/2)B(1/4)C4D1A long straight wire of a circular cross-section (radius a) carries a steady current I and the current I is uniformly distributed across this cross-section. Which of the following plots represents the variation of magnitude of magnetic field B with distance r from the centre of the wire?
A B
B C
C D
D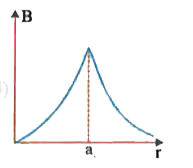
Figure show a long straight wire of a circular a cross-section with radius 'a' carrying steady curent I. The curent I is uniformaly distributed across this c ross -section.Calclulate the magnetic field in the regionr1<aandr2> a.
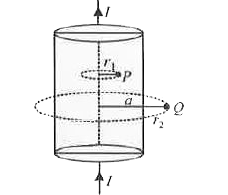
View SolutionThe adjoining figure shows a long straight wire of a circular cross section (radius a) carrying steady current I. The current I is uniformly distributed across its cross section. Calculate the magnetic field at a distance from its axis for (i)r<a,(ii)r>a.
View SolutionWrite Ampere's circuital law.A long straight wire of a circular cross section (radius a) carrying steady current.Current is uniformly distributed in the wire.Calculate magnetic field inside the region (r<a) in the wire.
View SolutionFigure shows a long straight wire of a circular cross-section (radius a) carrying steady current l. The current l is uniformly distributed across this cross-section. Calculate the magnetic field in the region r<aandr>a

View SolutionA long straight wire of a circular cross-section (radius r) carries a steady current I. The current is distributed uniformly across the cross-section. Calculare the magnetic field at a point (a) outside the wire , (b) inside the wire. Draw a graph showing variation of magnetic field.
View Solution
