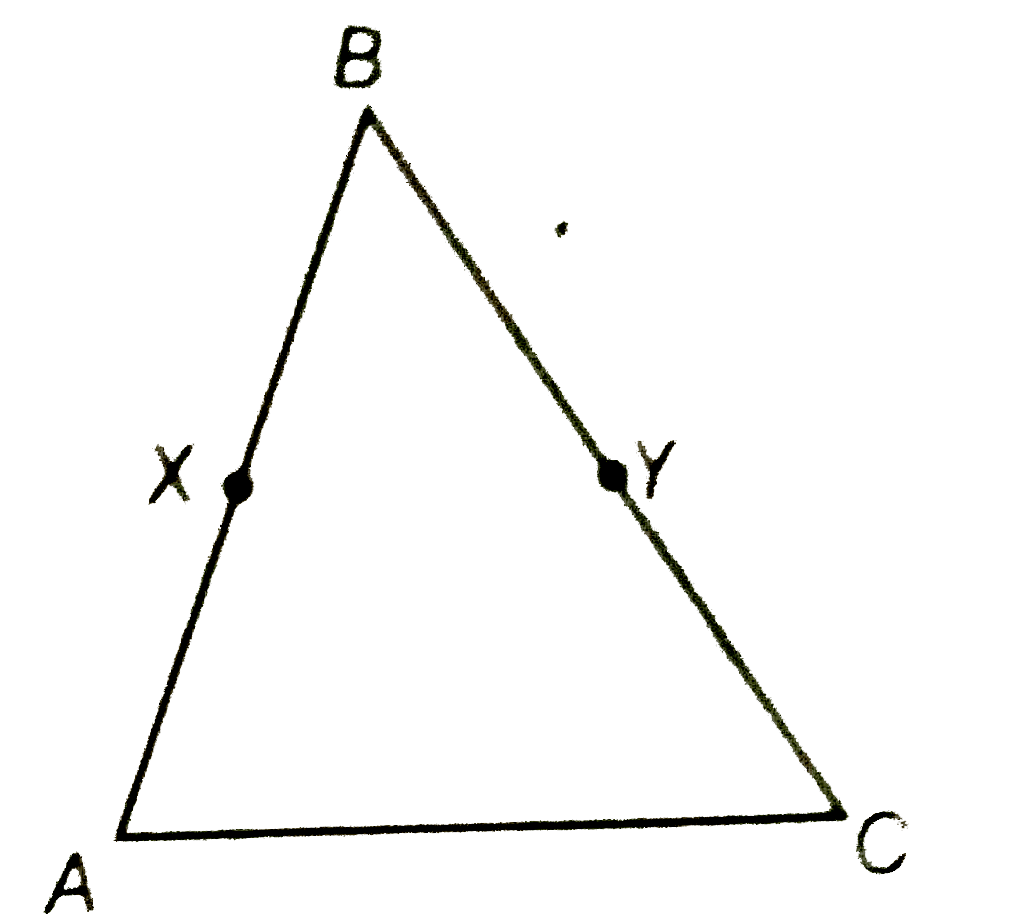
In the adjoining figure , we have X and Y are the mid - point of AC and BC and AX = CY . Show that AC =BC.
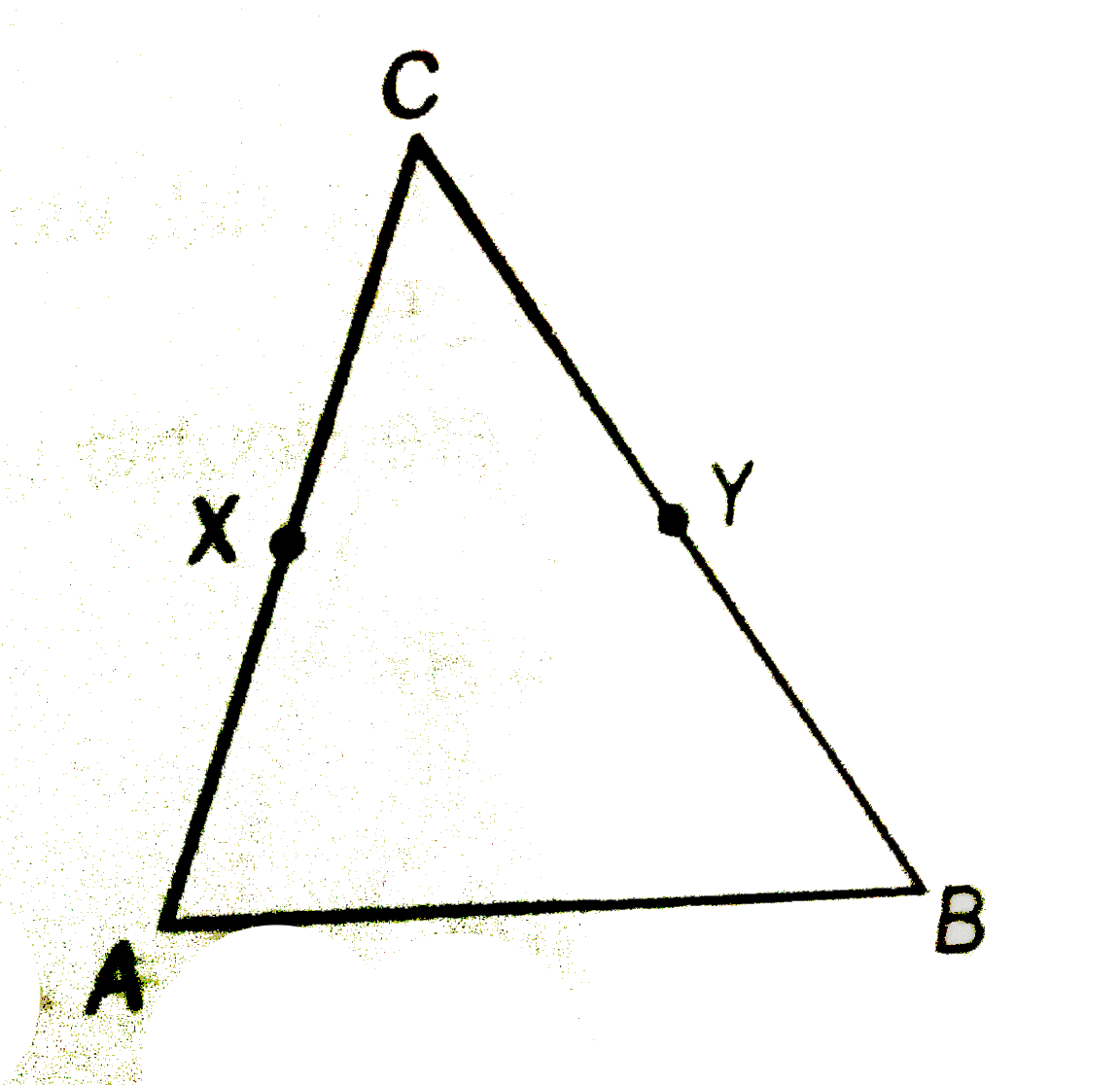
Given , X is the mid - point of AC.
∴AX=CX=12AC
⇒ 2AX=2CX=AC ...(i)
and Y is the mid -point of BC.
∴BY=CY=12BC
⇒ 2BY=2CY=BC ...(ii)
Also, given AX=CY ...(iii)
According to Euclid's axiom, things which are double of the same things are equal to one another.
From Eq. (iii), 2AX=2CY
⇒ AC=BC ["from Eqs. ("i) and (ii)"]
Topper's Solved these Questions
Similar Questions
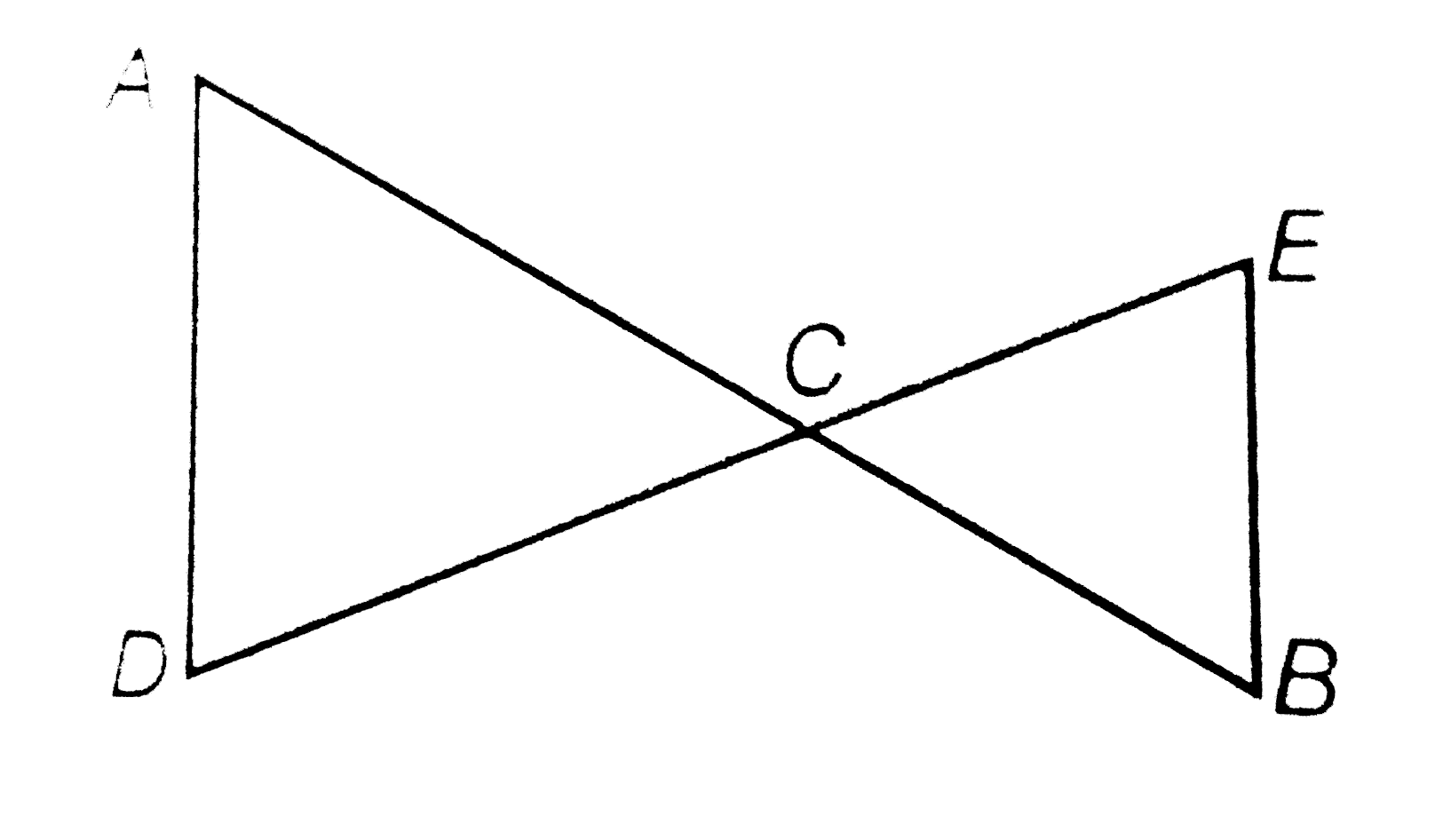
In the adjoining figure , we have AC=DC and CB = CE. Show that AB=DE.
View SolutionIn the adjoining figure D, E and F are the mid - points of the sides BC, AC and AB respectively to triangle. Show that ∠EDF=∠A, ∠DEF=∠B and ∠DFE=∠C:

View SolutionIn the adjoining figure
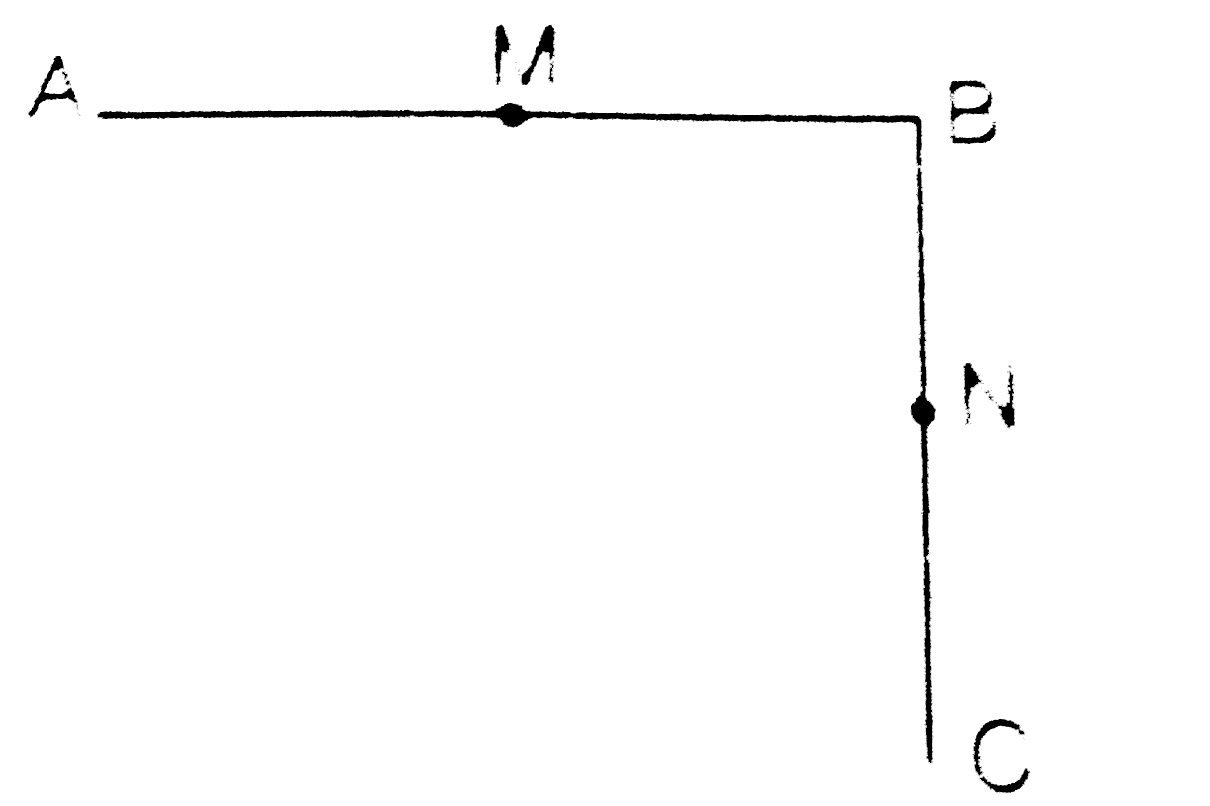
(i) AB=BC, M is the mid -point of AB and N is the mid- point of BC. Show that AM=NC.
(ii) BM=BN,M is the mid- point of AB and N is the mid - point of BC. Show that AB=BC.
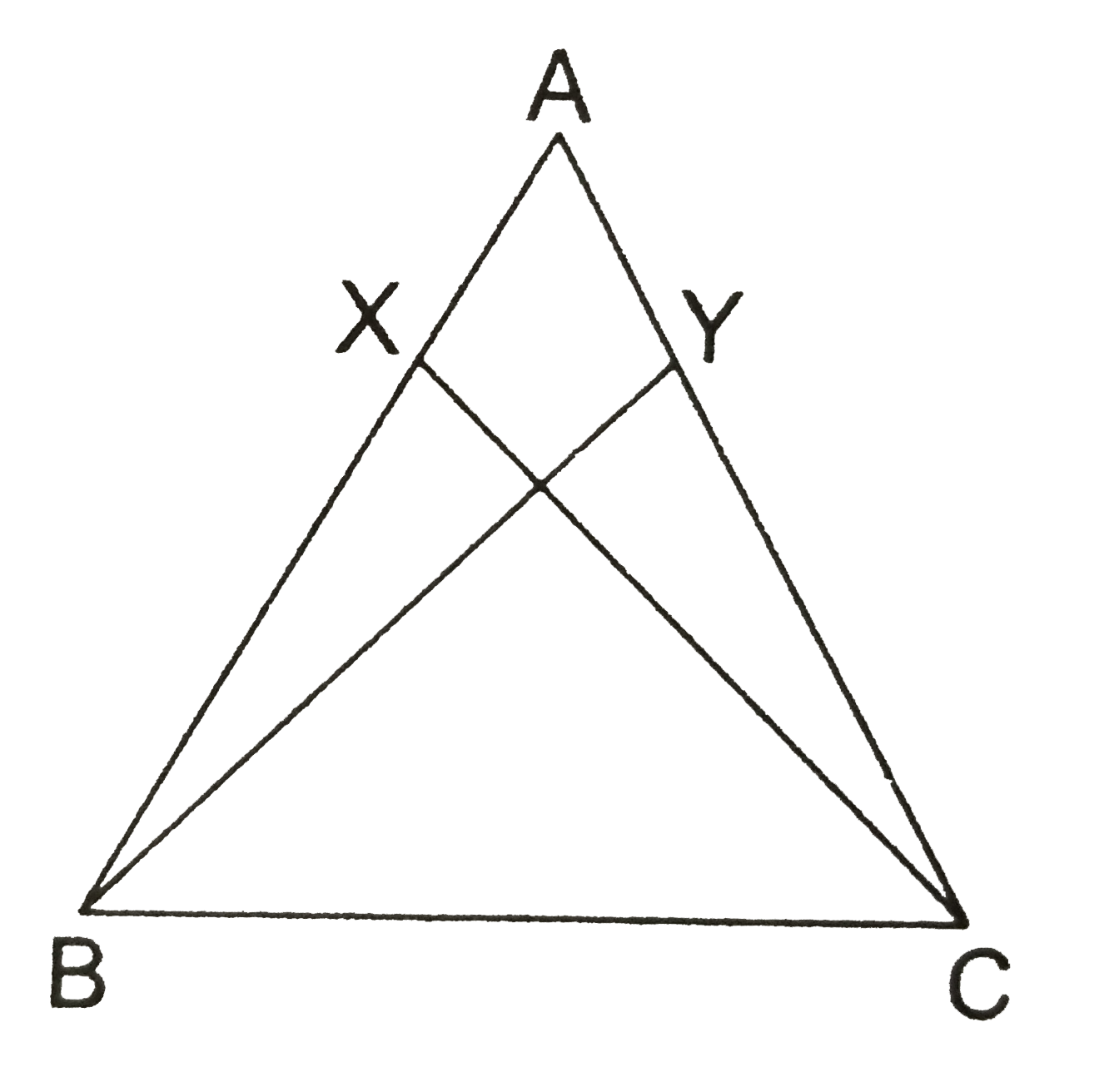
View SolutionIn the adjoining figure, X and Y are respectively two points on equal sides AB and AC of ΔABC such that AX = AY. Prove that CX = BY.
View SolutionIn the adjoining figure, x>y, Prove that AB>AC
View SolutionIn the adjoining figure, if AB = BC and BX =BY, then show that AX=CY
View SolutionIn the adjoining figure D, E and F are the mid-points of the sides BC, AC and AB respectively. △DEF is congruent to triangle :

View SolutionIn the adjoining figure, X and Y are respectively two points on equal sides AB and AC of ΔABC such that AX=AY. Prove that CX=BY.
View SolutionIn the adjoining figure AB= AC and D is the mid-point of BC. Use SSS rule of congruency to show that △ABD≅△ACD AD is bisector of ∠A AD is perpendicular to BC
View SolutionIn the adjoining figure, ΔABC is right angled at C and M is the mid-point of hypotenuse AB, If AC = 32 cm and BC = 60 cm, then find the length of CM.

View Solution

