Look at the adjoining figure. Show that length AH gt sum of lengths of AB + BC + CD
To show that the length AH is greater than the sum of the lengths AB+BC+CD, we can follow these steps:
1. Identify the segments: We have segments AB, BC, and CD that are part of a longer segment AD which is also part of AH.
2. Express the relationship: We can express the total length of segment AD as:
AD=AB+BC+CD
3. Recognize the relationship between segments: Since AD is part of AH, we have:
AH=AD+DH
where DH is another segment that extends from point D to point H.
4. Apply Euclid's fifth axiom: According to Euclid's fifth axiom, the whole is greater than the part. Therefore, since AH is the whole and AD is a part of AH:
AH>AD
5. Substitute the expression for AD: From step 2, we know that AD=AB+BC+CD. Thus, we can substitute this into our inequality:
AH>AB+BC+CD
6. Conclusion: We have shown that:
AH>AB+BC+CD
which is what we needed to prove.
AD=AB+BC+CD
AH=AD+DH
where DH is another segment that extends from point D to point H.
AH>AD
AH>AB+BC+CD
AH>AB+BC+CD
which is what we needed to prove.
Topper's Solved these Questions
Similar Questions
Knowledge Check
In the adjoining figure AB∣∣CDandPQ=SR, then :
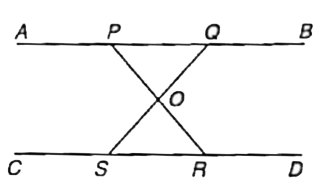 APQ=PSBSR=RPCPS=QRDAP=RD
APQ=PSBSR=RPCPS=QRDAP=RD
In given figure, show that AB || CD
View SolutionIn the adjoining figure , we have X and Y are the mid - point of AC and BC and AX = CY . Show that AC =BC.
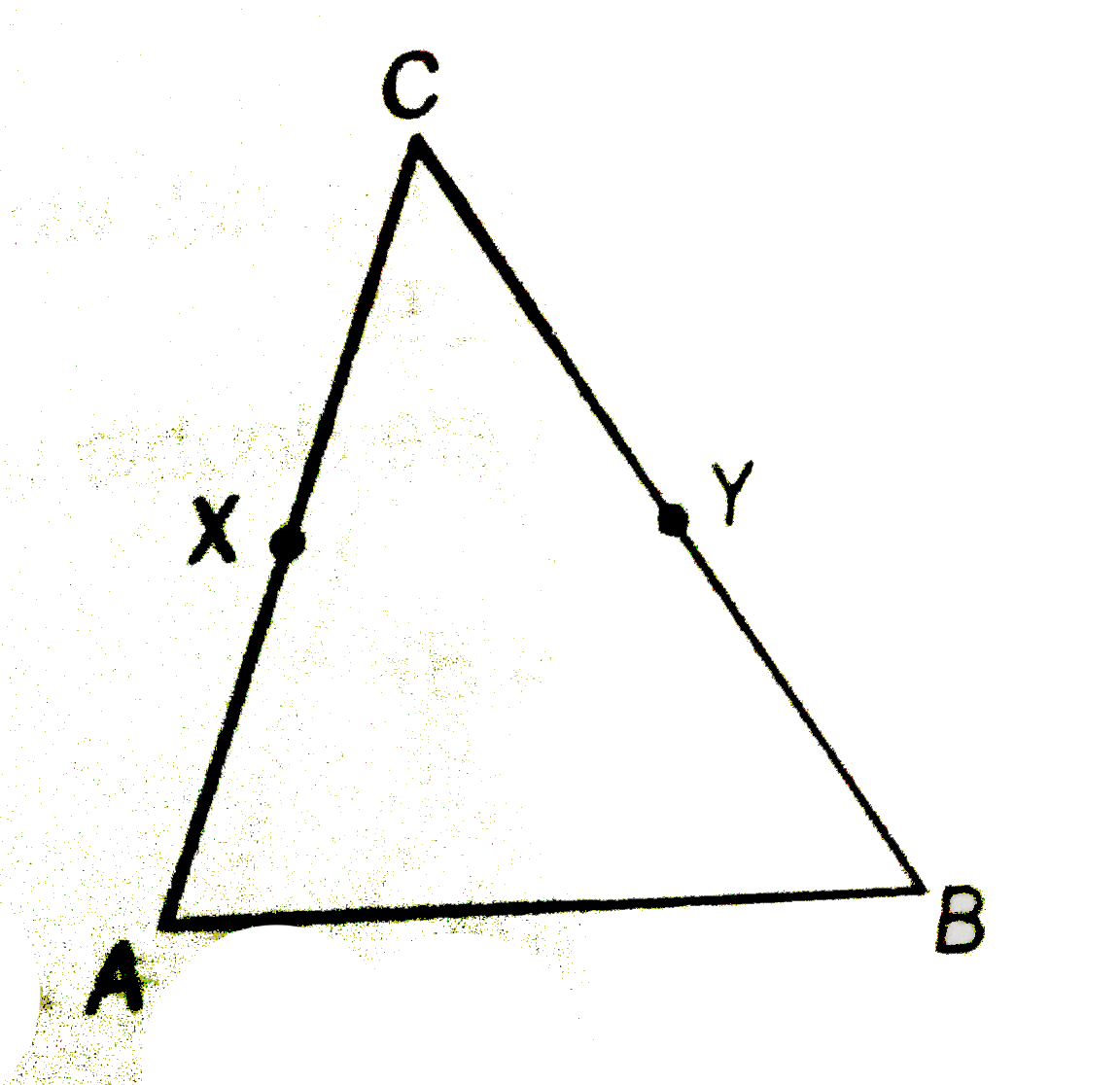
View SolutionIn the adjoining figure AB||CD .Find the value of x
View SolutionIn the adjoining figure AB||CD, find x and y

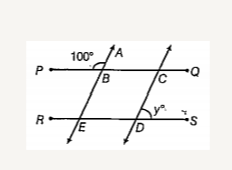
View SolutionIn the adjoining figure AE||CD and BC||ED, then find Y.
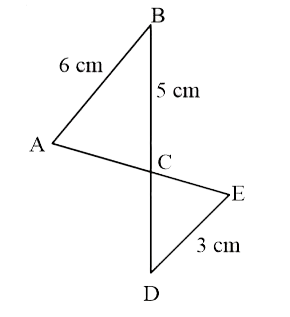
View SolutionIn the given figure, AB || DE. Find the length of CD.
View SolutionIn the adjoining figure, O is the centre of a circle in which AB and CD are two diameters. Prove that AC| |BD and AD| |BC. If ∠OBD=50∘, then find the value of ∠AOC.

View Solution