Attempt to prove Euclid 's fifth postulate using the other postulates and axioms led to the discovery of several other geometries.
The correct Answer is:1
All attempts to prove the fifth postulate as a theorem led to a great achievement in the creation of several other geometries. These geometries are quite different from Euclidean geometry and called non - Euclidean geometry.
Topper's Solved these Questions
Similar Questions
Knowledge Check
The postulate of Bohr theory that electrons jump from one orbit to the other, rather than flow is according to
AThe quantisation conceptBThe wave nature of electronCThe probability expression for electronDHeisenberg uncertainty principle(A) inside the auditorium
(B) other people
(C ) apart from us
(D) there were severalACDBABABDCCCBDADBDAC
How would you rewrite Euclid’s fifth postulate so that it would be easier to understand?
View SolutionProve that in a right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides. Using the above, solve the following: A ladder reaches a window which is 12 m above the ground on one side of the street. Keeping its foot at the same point, the ladder is turned to the other side of the street to reach a window 9m high. Find the width of the street if the length of the ladder is 15 m
View SolutionIntroduction|Definitions Of Euclid's |Axioms And Postulates|Axioms, Postulates And Theorems
View SolutionConsider two ‘postulates’ given below:(i) Given any two distinct points A and B, there exists a third point C which is in between A and B.(ii) There exist at least three points that are not on the same line. Do these postulates contain any undefined terms? Are these postulates consistent? Do they follow from Euclid’s postulates? Explain.
View SolutionProve that, if a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, the other two sides are divided in the same ratio.
Using the above result, do the following:
In Fig. 7 .45 DE||BC and BD = CE. Prove that ΔABC is an isosceles triangle.
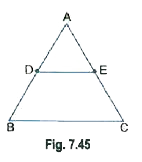
View SolutionIn a triangle, if the square on one side is equal to the sum of the squares on the other two sides, prove that the angle opposite to the first side is a right angle. Use the above theorem to find the measure of ∠PKR in Fig. 7.52.

View Solution
