Question

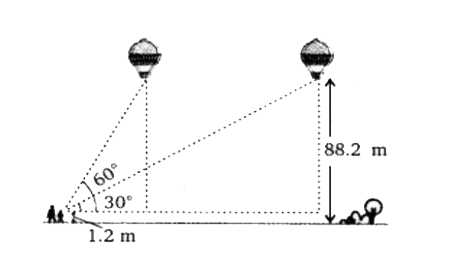
A 1.2 m tall girl
spots a balloon moving with the wind in a horizontal line at a height of 88.2
m from the ground. The angle of elevation of the balloon from the eyes of the
girl at any instant is $60o$
. After some
time, the angle of elevatio

Explanation

To solve the problem, we will break it down step by step.

Step 1: Understand the scenario
We have a girl who is 1.2 m tall, and she spots a balloon at a height of 88.2 m from the ground. The angle of elevation from her eyes to the balloon is initially 60 degrees.

Step 2: Determine the height of the balloon above the girl
The height of the balloon above the girl can be calculated as follows:
\( \text{Height of the balloon above the girl} = \text{Height of the balloon} - \text{Height of the girl} = 88.2 \, \text{m} - 1.2 \, \text{m} = 87 \, \text{m} \)

Step 3: Set up the right triangle for the first position (angle of elevation = 60 degrees)
Let:
- \( A \) be the position of the balloon,
- \( C \) be the position of the girl,
- \( D \) be the point directly below the balloon on the ground.

In triangle \( ACD \):
- \( AD \) (the height of the balloon above the girl) = 87 m
- Angle \( ACD \) = 60 degrees

Using the tangent function:
\( \tan(60^\circ) = \frac{AD}{CD} \implies CD = AD \cdot \tan(60^\circ) \)
Since \( \tan(60^\circ) = \sqrt{3} \):
\( CD = 87 \cdot \sqrt{3} \)

Step 4: Set up the right triangle for the second position (angle of elevation = 30 degrees)
Now, after some time, the angle of elevation reduces to 30 degrees. Let \( E \) be the new position of the balloon.

In triangle \( BCE \):
- \( BE \) (the height of the balloon above the girl) = 87 m
- Angle \( BCE \) = 30 degrees

Using the tangent function again:
\( \tan(30^\circ) = \frac{BE}{CE} \implies CE = BE \cdot \tan(30^\circ) \)
Since \( \tan(30^\circ) = \frac{1}{\sqrt{3}} \):
\( CE = 87 \cdot \frac{1}{\sqrt{3}} = \frac{87}{\sqrt{3}} = 29 \sqrt{3} \)

Step 5: Calculate the distance traveled by the balloon
The distance traveled by the balloon, \( DE \), is the difference between \( CE \) and \( CD \):
\( DE = CE - CD = (87 \cdot \frac{1}{\sqrt{3}}) - (87 \cdot \sqrt{3}) = 87 \left(\frac{1}{\sqrt{3}} - \sqrt{3}\right) \)
To simplify:
\( DE = 87 \left(\frac{1 - 3}{\sqrt{3}}\right) = 87 \left(\frac{-2}{\sqrt{3}}\right) = -\frac{174}{\sqrt{3}} \)
Since distance cannot be negative, we take the absolute value:
\( DE = \frac{174}{\sqrt{3}} \approx 100.58 \, \text{m} \)

Final Answer
The distance traveled by the balloon during the interval is approximately \( 100.58 \, \text{m} \).

---