A boy whose eye level is 1.3m from the ground, spots a balloon moving with the wind in a horizontal line at same height from the ground. The angle of elevation of the balloon from the eyes of the boy at an instant is 60∘. After 2 seconds, the angle of elevation reduces to 30∘. If the speed of the wind is 29√3m/s then find the height of the balloon from the ground.
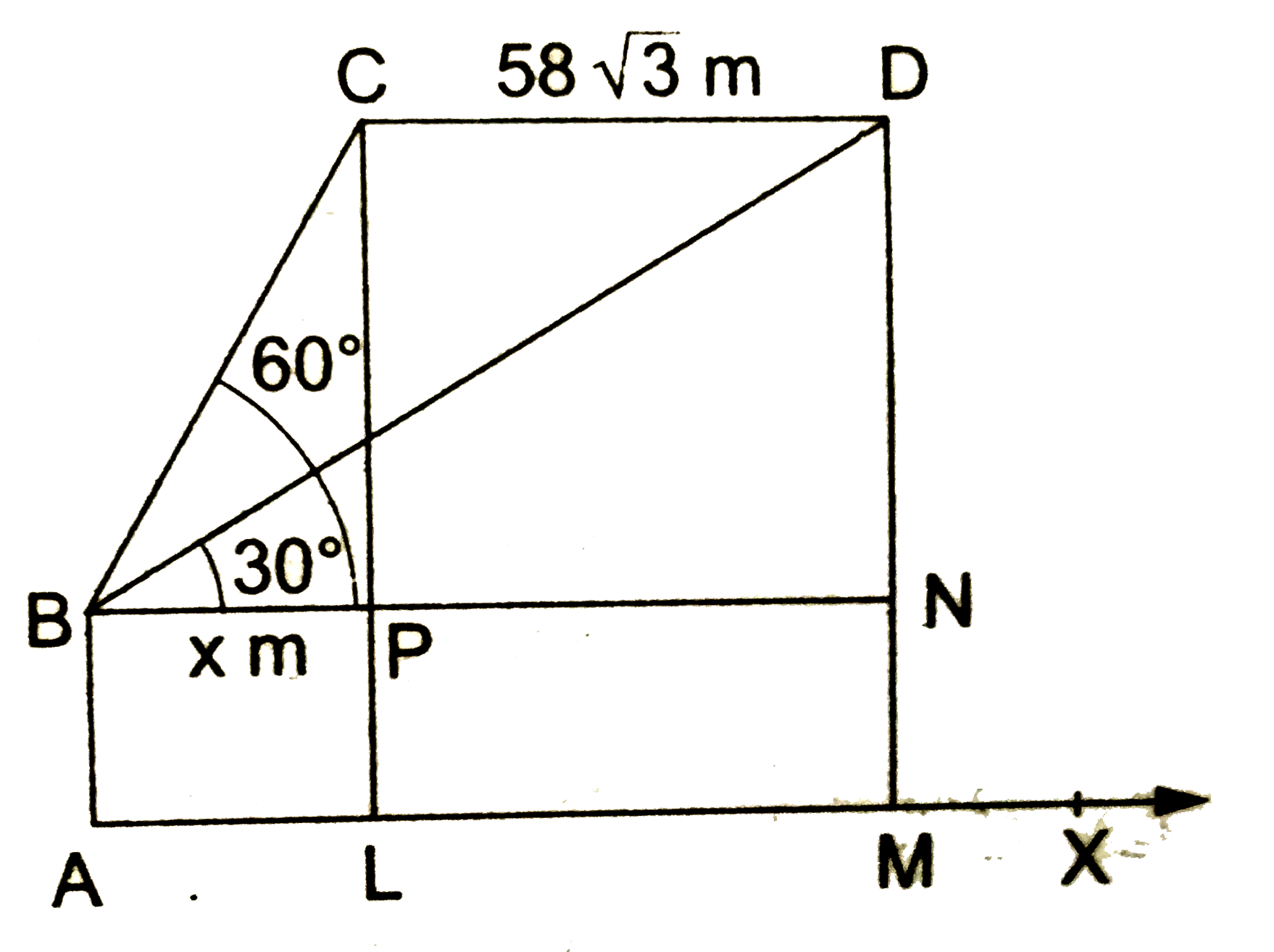
Let AB be the position of the boy and AX be the the horizontal grund. Let C and D be the two positions of the ballon. Draw CL⊥AX,DM⊥AX and BN⊥DM, intersecting CL at P. Then ∠CBN=60∘ and ∠DBN=30∘.
Distance covered by the balloon in 2 seconds.
=(29√3×2)m=58√3m.
∵CD=58√3.
Let BP=x metres, Then,
BN=(BP+PN)=(BP+CD)=(x+58√3)mandDN=CP From right ΔBND, we have
DNBN=tan30∘=1√3.
⇒DN(x+58√3)m=1√3⇒DN=(x+58√3)√3m........(i)
From right ΔBPC, we have
CPBP=tan60∘=√3
⇒CPxm=√3⇒CP=(x√3)
⇒(3x−x)=58√3⇒2x=58√3⇒x=29√3.
From (ii), we get
CP=(29√3×√3)m=(29×3)m=87m
∴ height of the ballon from the ground.
=CL=CP+PL=CP+AB=87m+1.3m=88.3m
Hence, the height of the balloon from the ground is 88.3 metres.
Topper's Solved these Questions
- HEIGHTS AND DISTANCESBOOK - RS AGGARWALCHAPTER - HEIGHTS AND DISTANCESEXERCISE - Exercise 14
38 Videos
- HEIGHTS AND DISTANCESBOOK - RS AGGARWALCHAPTER - HEIGHTS AND DISTANCESEXERCISE - Multiple Choice Questions (Mcq)
25 Videos
- COORDINATE GEOMETRYBOOK - RS AGGARWALCHAPTER - COORDINATE GEOMETRYEXERCISE - Multiple Choice Questions (Mcq)
34 Videos
- LINEAR EQUATIONS IN TWO VARIABLES BOOK - RS AGGARWALCHAPTER - LINEAR EQUATIONS IN TWO VARIABLES EXERCISE - QUESTION
2 Videos
Similar Questions
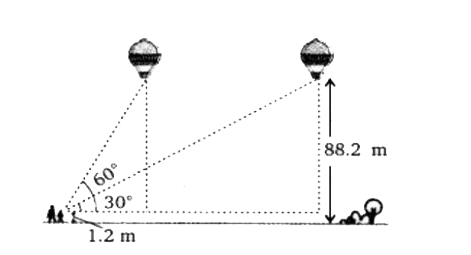
A 1.2 m tall girl spots a ballon moving with wind in a horizontal line at a height of 88.2 m from the ground. The angle of elevation of the balloon from the eyes of the girl at any instant is 60∘. After some time, the angle of elevation reduces to 30∘. Find the distance travelled by the balloon during the interval.
View SolutionA 1.2 m tall girl spots a ballon moving with the wind in a horizontal line at a height of 88.2 m from a ground. The angle of elevation of the balloon from the eyes of the girl at any instant is 600. After some time, the angle of elevation reduces to 300. Find the distance travelled by the balloon during the interval.
View Solution
Knowledge Check
The angle of elevation of an airplane from a point on the ground is 60∘. After a flight of 30 seconds, the angle of elevation becomes 30∘. If the airplane is flying at a constant height of 3000√3m, find the speed of the airplane.
A200m/sB250m/sC350m/sD300m/sThe angle of elevation of an aeroplane from a point on the ground is 60∘ .After flying for 30 seconds ,the angle of elevation changes to 30∘ .If the aeroplane is flying at a height of 1500√3 metre , then what is the speed (in m/s) of aeroplane?
A50B100C200D300The angle of elevation of the top of a tower at a point G on the ground is 30∘. On walking 20 m towards the tower the angle of elevation becomes 60∘. The height of the tower is equal to :
A10/√3mB20√3mC20/√3mD10√3m
A 1.2m tall girl spots a balloon moving with the wind in a horizontal line at a height 88.2 m from the ground. The angle of elevation of the balloon from the eyes of the girl at any instant is 60°.After sometime, the angle of elevation reduces 30°.Find the distance travelled by the balloon during the interval.
View SolutionThe angle of elevation of an aeroplane from a point P on the ground is 60∘. After a flight of 15 seconds, the angle of elevation changes to 30∘. If the aeroplane is flying at a constant height of 1500√3 m, find the speed of the aeroplane
View SolutionThe angle of elevation of a jet plane from a point A on the ground is 60o . After a flight of 30 seconds, the angle of elevation changes to 30o . If the jet plane is flying at a constant height of 3600√3m , find the speed of the jet plane.
View SolutionThe angle of elevation of the top of a tower at a point on the ground is 30∘. If on walking 20 m toward the tower, the angle of elevation becomes 60∘, then the height of the tower is
View SolutionThe angle of elevation of an aeroplane from a point on the ground is 60∘ . After flying for 30 seconds, the angle of elevation charges to 30∘ . If the aeroplane is flying at a height of 4500 m, then what is the speed (in m/s) of aeroplane
View Solution
