A man pushes a cylinder of mass m1 with the help of a plank of mass m2 as shown in figure. There in no slipping at any contact. The horizontal component of the force applied by the man is F.
(a) the acceleration fo the plank and the center of mass of the cylinder, and
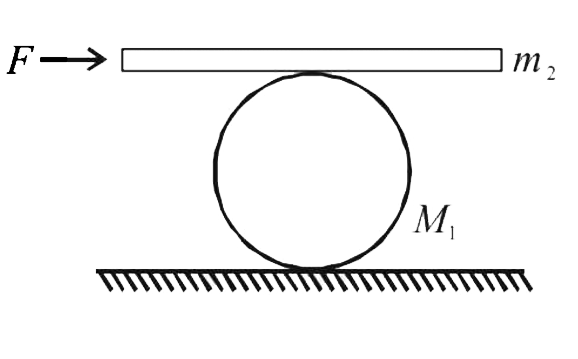
(b) the magnitudes and direction of frictional force at contact points.
(i) 8F3m1+8m2, (ii) 4F3m1+8m2, (iii) 3Fm13m1+8m2, (iv) Fm13m1+8m2
The man applies a force F in the horizontal direction on the plank as shown in the figure. Therefore, the point of contact of the plank with the cylinder will try to move towards the right. Therefore, the friction force f will act towards the left on the plank.
To each and every action, there is an equal and opposite reaction. Therefore, a frictional force f will act on the top of the cylinder towards the right.
Direction of friction by surface on cylinder:
For finding the direction on the cylinder, the force f is trying to move the point of contact towards right by an acceleration aCM=fm1 acting towards the right.
At the same time, the force f is trying to rotate the cylinder about its centre of mass in the clockwise direction.
f×R=I×α⇒α=f×RI=f×R12m1R2=2fm1R
Therefore, acceleration of the point of contact, ap=aCM−αR=fm1−2fm1R×R=−fm1
i.e., towards the left.
Therefore, the point of contact of the cylinder with the ground move towards the left. Therefore, friction force acts towards the right on the cylinder.
Applying Newton's law on the plank, we get
F−f=m2a2........(i)
Also a2=2a1............(ii)
Because a2 is the acceleration of the topmost point of the cylinder and there is no slipping.
Apply Newton's law on the cylinder.
f+f′=m1a1........(iii)
The torque equation for the cylinder is,
f×R−f×R=Iα=12m1R2×(a1R)(∴I=m1R2 and Rα=a1)
∴f−f'=12m1a1 ...........(iv)
Solving Eqs. (iii) and (iv), we get f=34m1a1 and f'=14m1a1
From Eqs. (i) and (ii), F−f=2m2a1⇒F=−34m1a1=2m2a1
∴a1=4F3m1+8m2 and a2=8F3m1+8m2
f=34m1×4F3m1+8m2 and f′=14m1×a1=Fm13m1+8m2.

Similar Questions
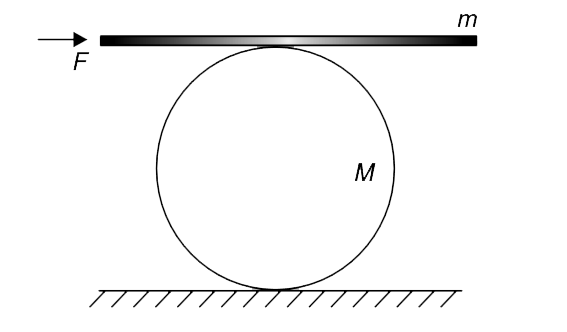
A boy pushes a cylinder of mass M with the help of a plank of mass m as shown in figure. There is no slipping at any contact. The horizontal component of the force applied by the boy on the plank is F. Find
(a) The acceleration of the centre of the cylinder
(b) The friction force between the plank and the cylinder
View SolutionA plank of mass m1 with a uniform sphere of mass m2 placed on it rests on a smooth horizontal plane. A constant horizontal force F is applied to the plank. With what acceleration will the plank and the centre of the sphere move provided there is no sliding between the plank and the sphere?
View Solution
Knowledge Check
A disc of mass m and radius R is placed over a plank of same mass m. There is sufficient friction between disc and plank to prevent slipping. A force F is applied at the centre of the disc.

Acceleration of the plank isAF2mB3F4mCF4mD3F2mThe mass m is placed on a body of mass M. There is no friction. The force F is applied on M on it moves with acceleration a. Then, the force on the top body is
 AFBmaCF - maDNone of these
AFBmaCF - maDNone of these

A cylinder is sandwiched between two planks. Two constant horizontal forces F and 2F are applied on the planks as shown. Determine the acceleration of the centre of mass of cylinder and the top plank. If there is no slipping at the top and bottom of cylinder.
View SolutionA solid sphere of mass m and radius R is placed over a plank of same mass m. There is sufficient friction between sphere and plank to prevent slipping.

When a horizontal force F is applied at centre of sphere, acceleration of the plank is
View SolutionA sphere of mass m and radius r is placed on a rough plank of mass M. The system is placed on a smooth horizontal surface. A constant force F is applied on the plank such that the sphere rolls purely on the plank. Find the acceleration of the sphere.

View SolutionA cylinder of mass 2kg and radius 10cm is held between two planks as shown in Fig. Calculate KE of the cylinder when there is no slipping at any point.

View SolutionA solid cylinder of mass M and radius 2R is rolled up on an incline with the help of a plank of mass 2M as shown in the figure. A constant force F is acting on the plank parallel to the incline. There is no slipping at any of the contact. The friction force between the plank and cylinder is given by:

View SolutionConsider a cylinder of mass M and radius R lying on a rough horizontal plane. It has a plank lying on its top as shown in the figure. A force F is applied on the plank such that the plank moves and causes the cylinder to roll. The plank always remains horizontal. There is no slipping at any point to contact.

(a) what are the directions of the fricition forces acting at A and B on the plank and the cylinder ?
(b) Calculate the acceleration of the cylinder.
(c) Find the value of frictional force at A & B.
View Solution
