A solid cylinder of mass M and radius 2R is rolled up on an incline with the help of a plank of mass 2M as shown in the figure. A constant force F is acting on the plank parallel to the incline. There is no slipping at any of the contact. The friction force between the plank and cylinder is given by:

$\frac{F}{2}$

$\frac{3 F + 29 M g sin θ}{57}$

$\frac{3 F + 2 M g sin θ}{19}$

Coefficient of friction value is not given and hence Cannot be found

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

Updated on:21/07/2023

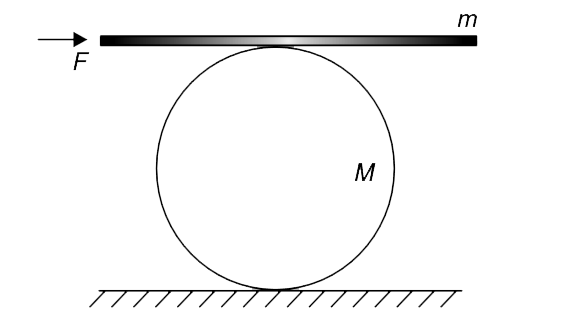
Consider a cylinder of mass $M = 1 k g$ and radius $R = 1 m$ lying on a rough horizontal plane. It has a plank lying on its stop as shown in the figure.

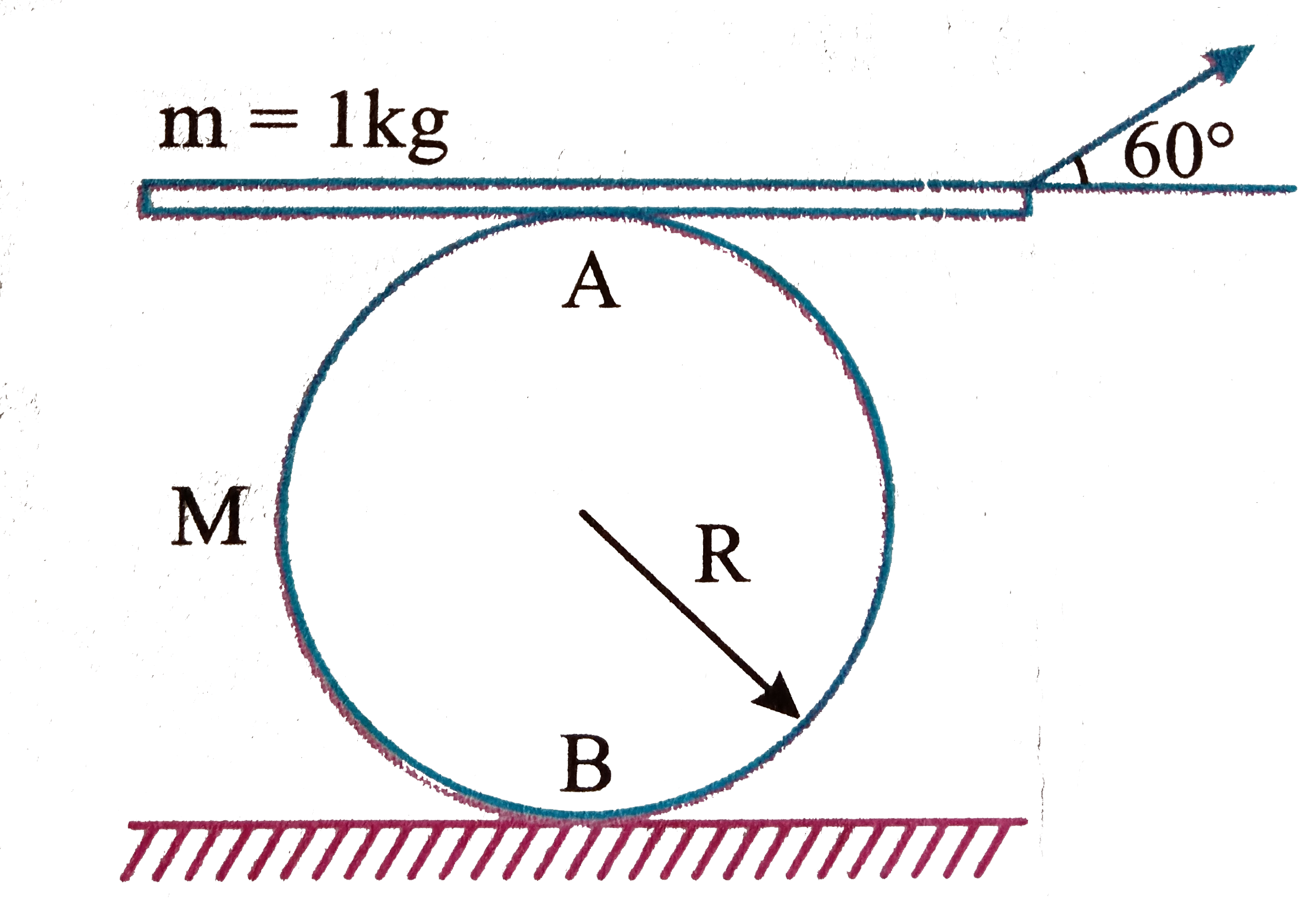
A force $F = 55 N$ is applied on the plank moves and causes the cylinder to roll. The plank always remains horizontal. there is no slipping at any point of contact.
The acceleration of cylinder is
A $20 m / s^{2}$
B $10 m / s^{2}$
C $5 m / s^{2}$
D $12 m / s^{2}$
A cylinder of radius R is to roll without slippoing between two planks as shown in the figure. Then
Aangular velocity of the cylinder is $\frac{v}{R}$ counter clockwise
Bangular velocity of the cylinder is $\frac{2 v}{R}$ clockwise
Cvelocity of centre of mass of the cylinder is $v$ towards left
Dvelocity of centre of mass of the cylinder is $2 v$ towards right.
Consider a cylinder of mass $M = 1 k g$ and radius $R = 1 m$ lying on a rough horizontal plane. It has a plank lying on its stop as shown in the figure.

A force $F = 55 N$ is applied on the plank moves and causes the cylinder to roll. The plank always remains horizontal. there is no slipping at any point of contact.
The value of frictional force at $A$ is
A $7.5 N$
B $5.0 N$
C $2.5 N$
D $1.5 N$