Find the emf (V) and internal resistance (R) of a single battery which is equivalent toa parallel combination of two batteries of emf V1 and V2 and internal resistances r1 and r2 respectively, with polrities as shown in figure
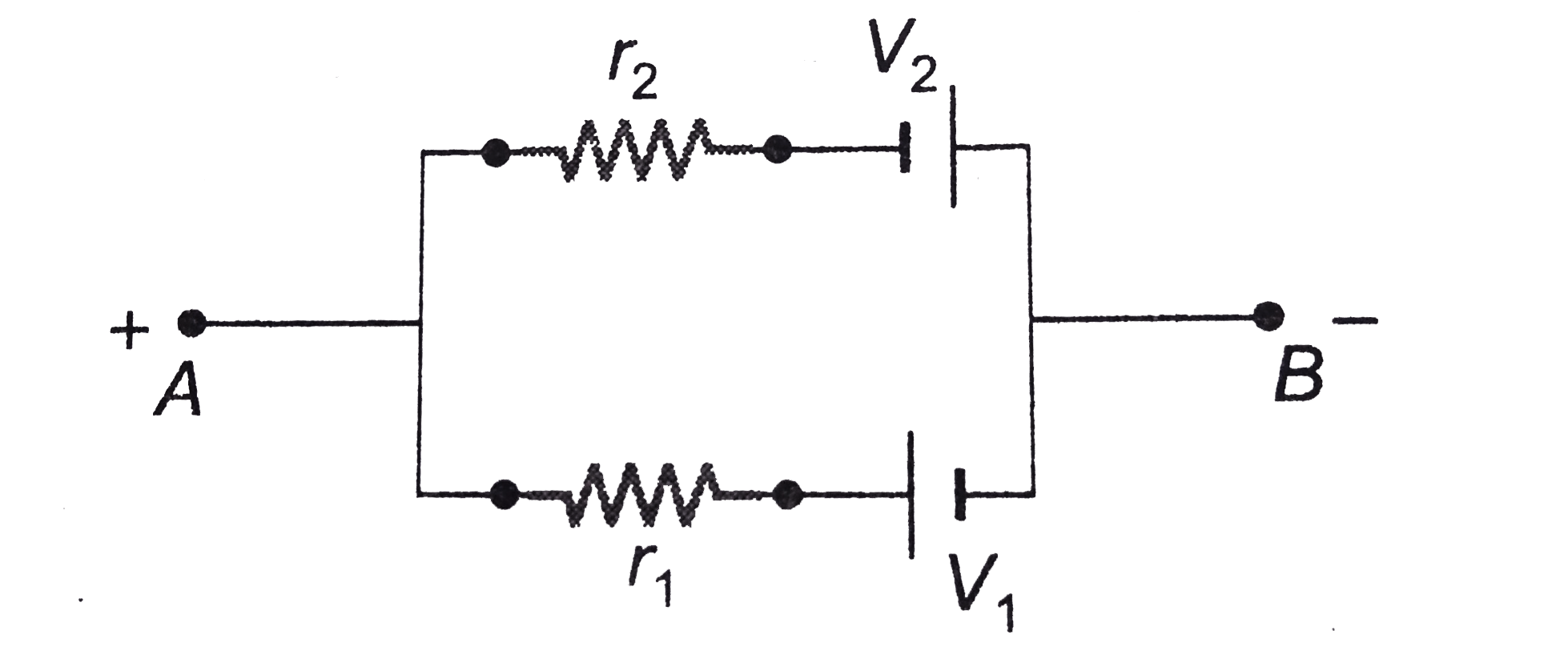
(a) Equivalent emf (V) of the battery
PD across the terminals of the battery is equal to its emf when current drawn from the battery is zero. In the given circuit, , Current in the internal circuit,
j=NetemfTotalresistance=V1+V2r1+r2
Therefore, potential difference between A and B would be
VA−VB=V1−ir1
∴VA−VB=V1−(V1+V2r1+r2)r1=V1r2−V2r1r1+r2=20×3−5×69=309=3.33
So, the equivalent emf of the battery is 3.33 V, Note that if V1r2=V2r1,V=0
If V1r2>V2r1,VA−VB= Positive i.e., A side of the equivalent battery will become the positive terminal and vice-versa.
(b)Internal resistance (r) of the battery
r1andr2 are in parallel. Therefore, the internal resistance r will be given by
1/r=1/r1+1/r2orr=r1r2r1+r2=6×36+3=2Ω
Similar Questions
Find the emf (V) and internal resistance (r) of a single battery which is equivalent to a parallel combination of two batteries of emf's V1,andV_(2), and internal resistance r1 and r2 respectively, with polarities as shown in the figure
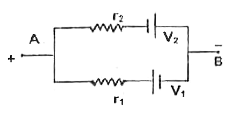
View Solution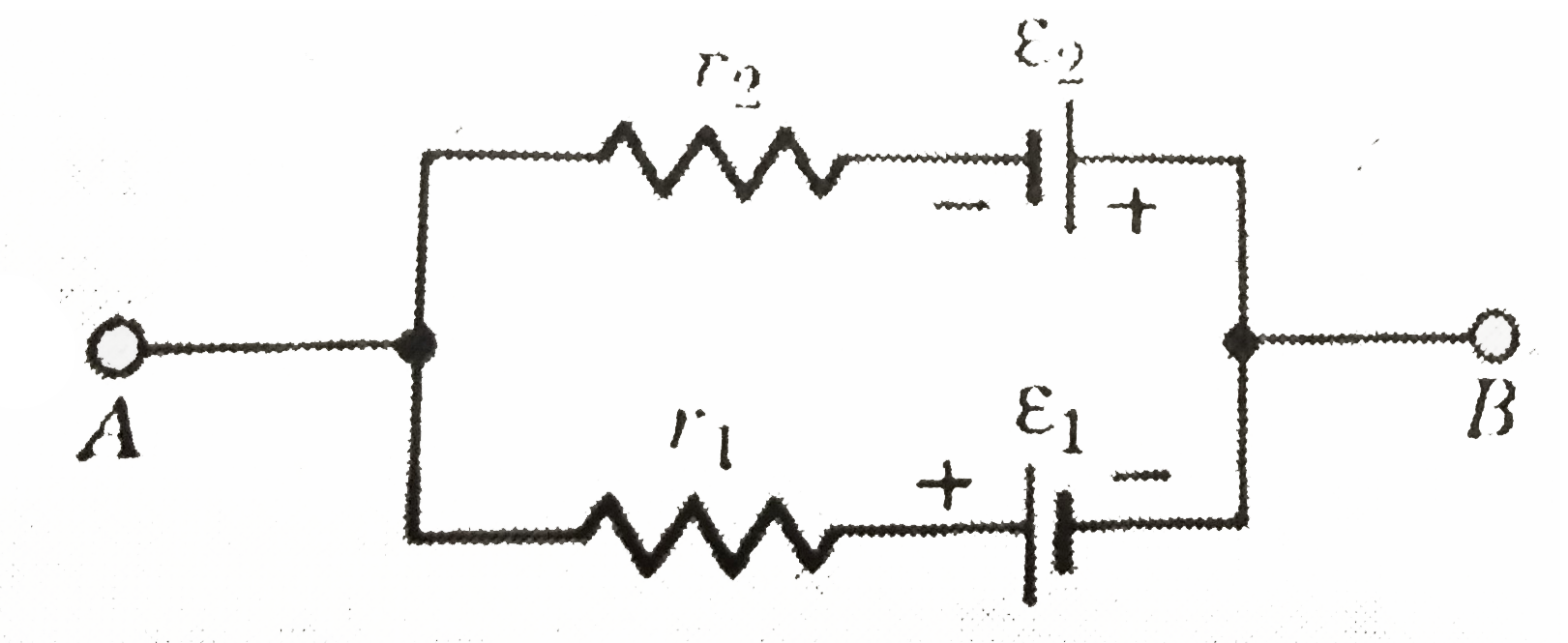
find the emf (ε0) and internal resistance (r0) if a battery which is equivalent to a parallel combination of two batteries of emfs ε1andε2 and internal resistances r1andr2 respectively, with polarities as shown in figure.
View Solution
Knowledge Check
Two batteries of emf ε1 and ε2(ε2>ε1) and internal resistances r_1 and r2 respectively are connected in parallel as shown in Fig. Then
 Athe equivalent emf εeq of the two cells is betweenε1 and ε2 i.e., ε1<εeq<ε2Bthe equivalent emf εeq is smaller than ε1Cthe εeq is given by εeq=ε1+ε2 always .Dεeq is independent of internal resistances r1 and r2
Athe equivalent emf εeq of the two cells is betweenε1 and ε2 i.e., ε1<εeq<ε2Bthe equivalent emf εeq is smaller than ε1Cthe εeq is given by εeq=ε1+ε2 always .Dεeq is independent of internal resistances r1 and r2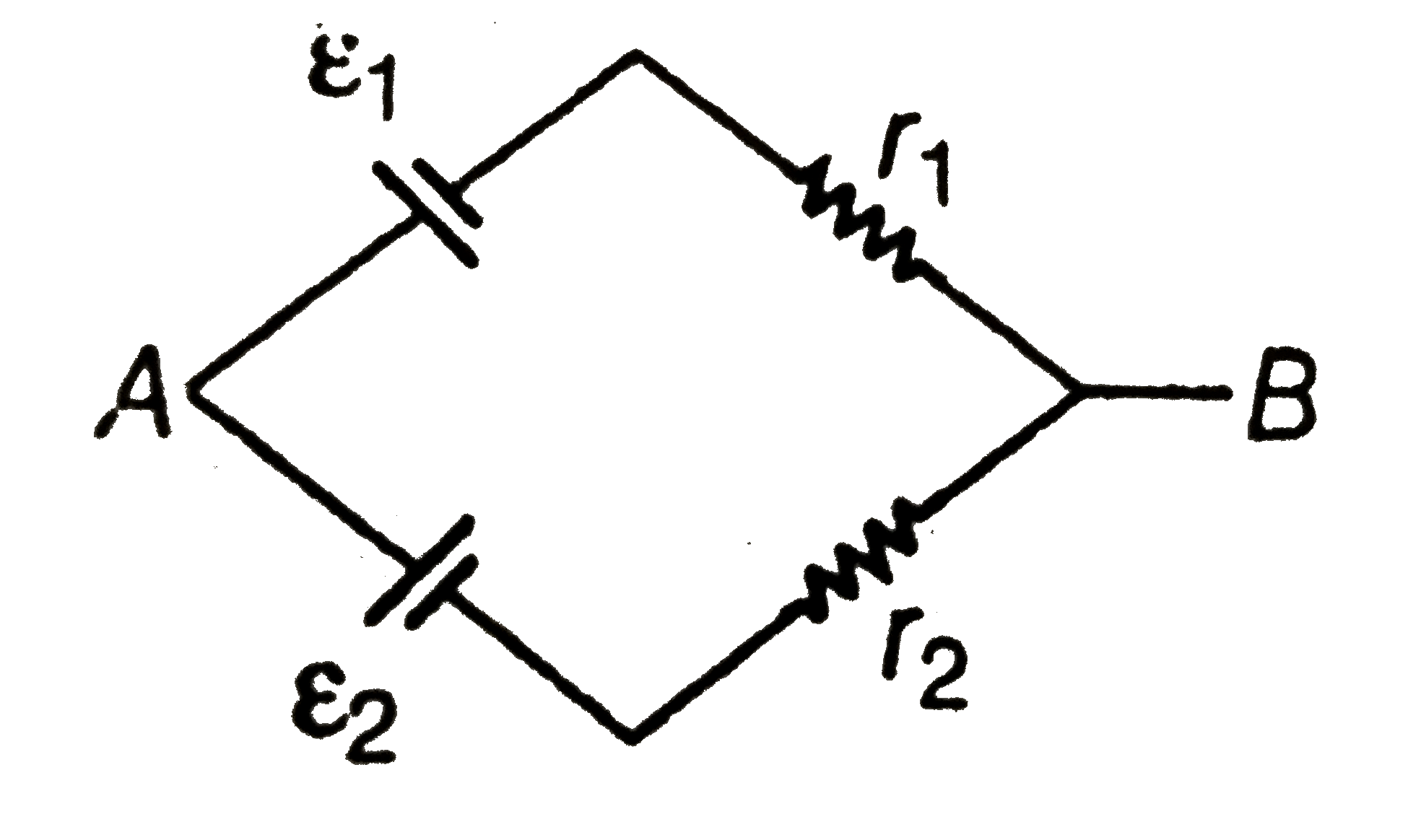
Two batteries of emf ε1andε2(ε2>ε1) and internal resistance r1andr2 respectively are connected in parallel as shown in figure.AThe equivalent emf εeq of the two cells is between ε1andε2, i.e., ε1<εeq<ε2Bthe equivalent emf εeq is smaller than ε1CThe εeq is given by εeq=ε1+ε2 always.Dεeq is independent of internal resistance r1andr2.A resistor R is conneted to a parallel combination of two identical batteries each with emf E and an internal resistance r. The potential drop across the resistance R is.
A2ER2R+rBER2R+rCER2R+rD2ERR+2r
Find the e.m.f(E0) end internal resistance (r0) of a simple battery which is equivalent to a perallel combination of two battery of e.m.fE1andE2 and internal resistance v1andv2 respectively with polarities
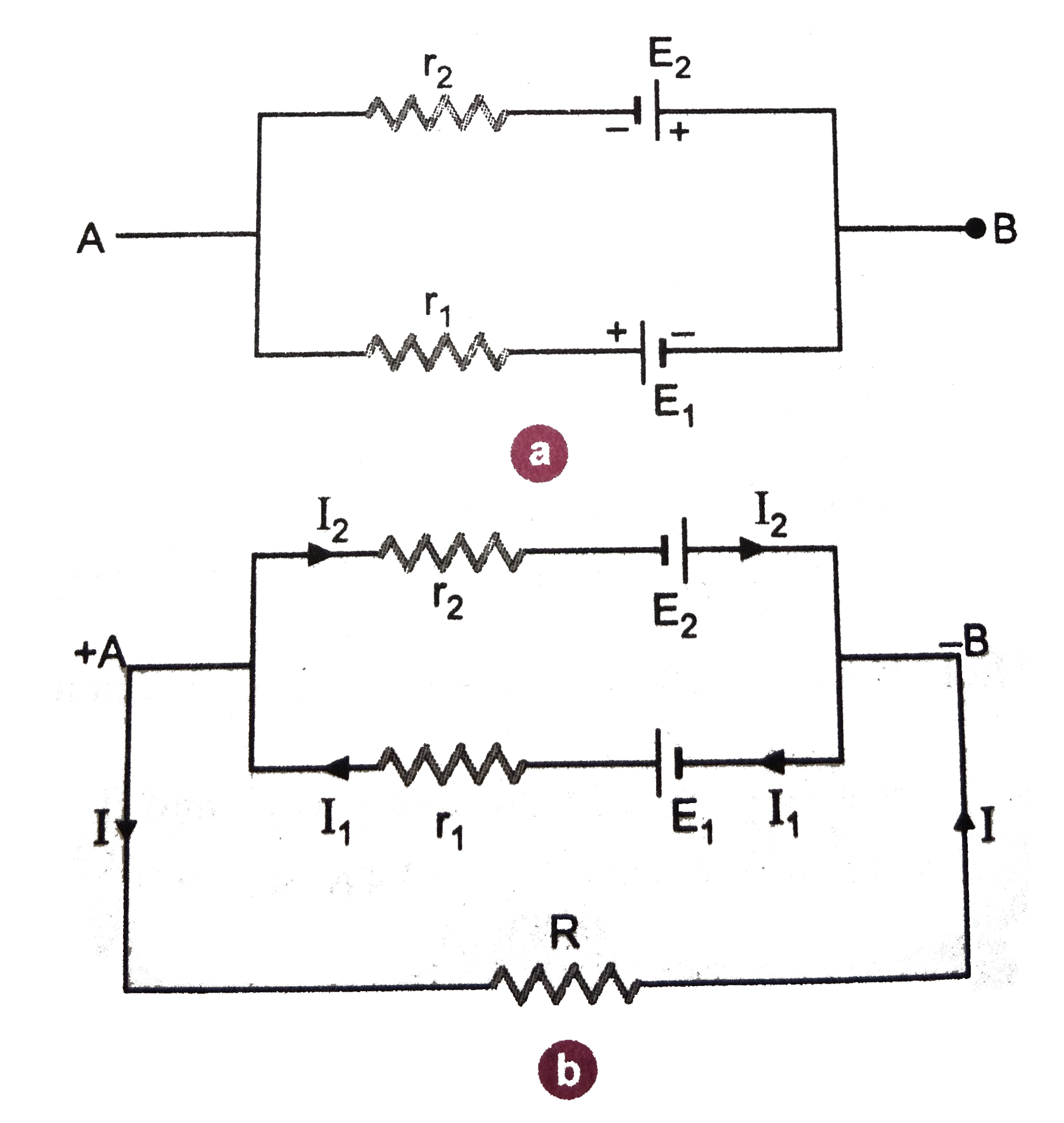
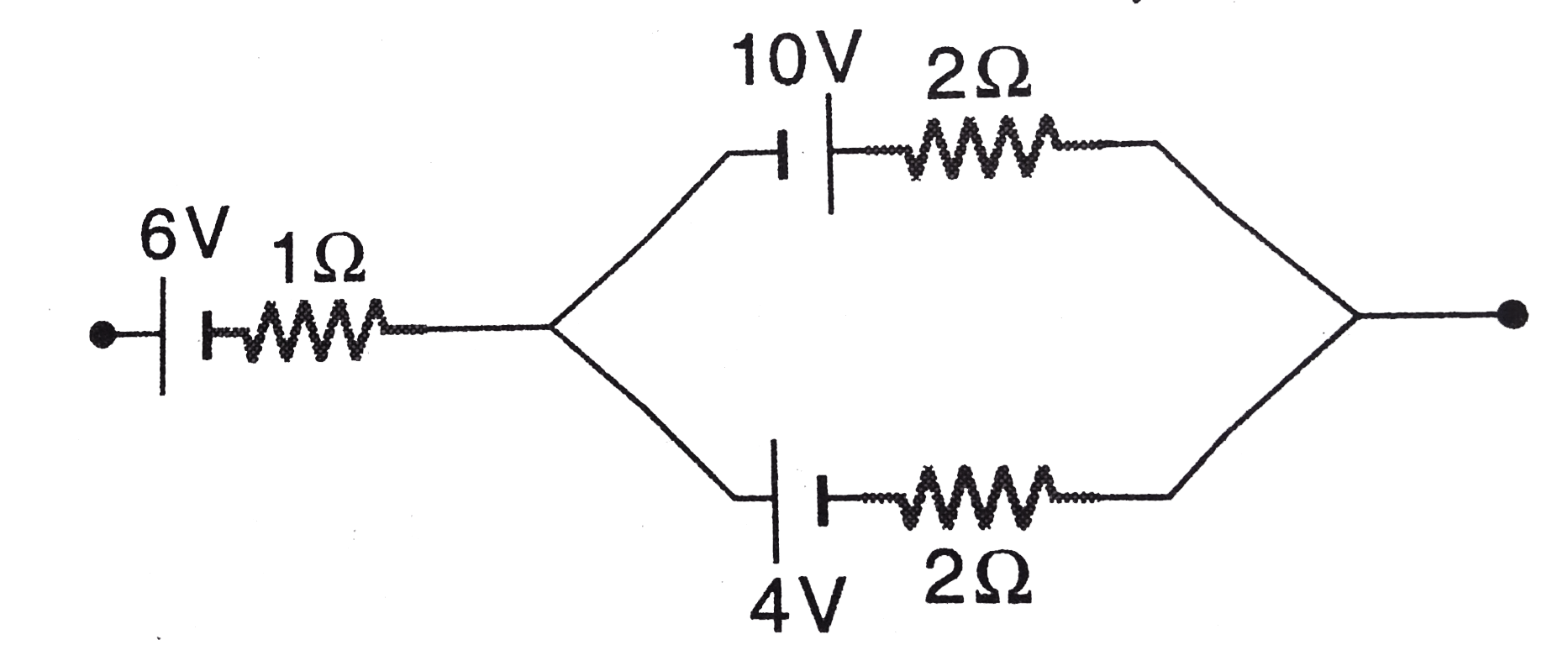
View SolutionFind the emf and internal resistance of a single battery which is equivalent to a combination of three batteries as show in figure.
View SolutionFind the emf ε and the internal resistance r of an electric source which is equivalent to two batteries of emf's ε1 and ε2 and internal resistances r1andr2, connected in parallel.
View SolutionFind the emf and the internal resistance of a source which is equivalent to two batteries connected in parallel whose emf's are equal to E1 and E2 and internal resistances to R1 and R2
View SolutionTwo batteries of e.m.f. E1 and E2 and internal resistance r1 and r2 are connected in parallel. Determine their equivelent e.m.f.
View Solution
