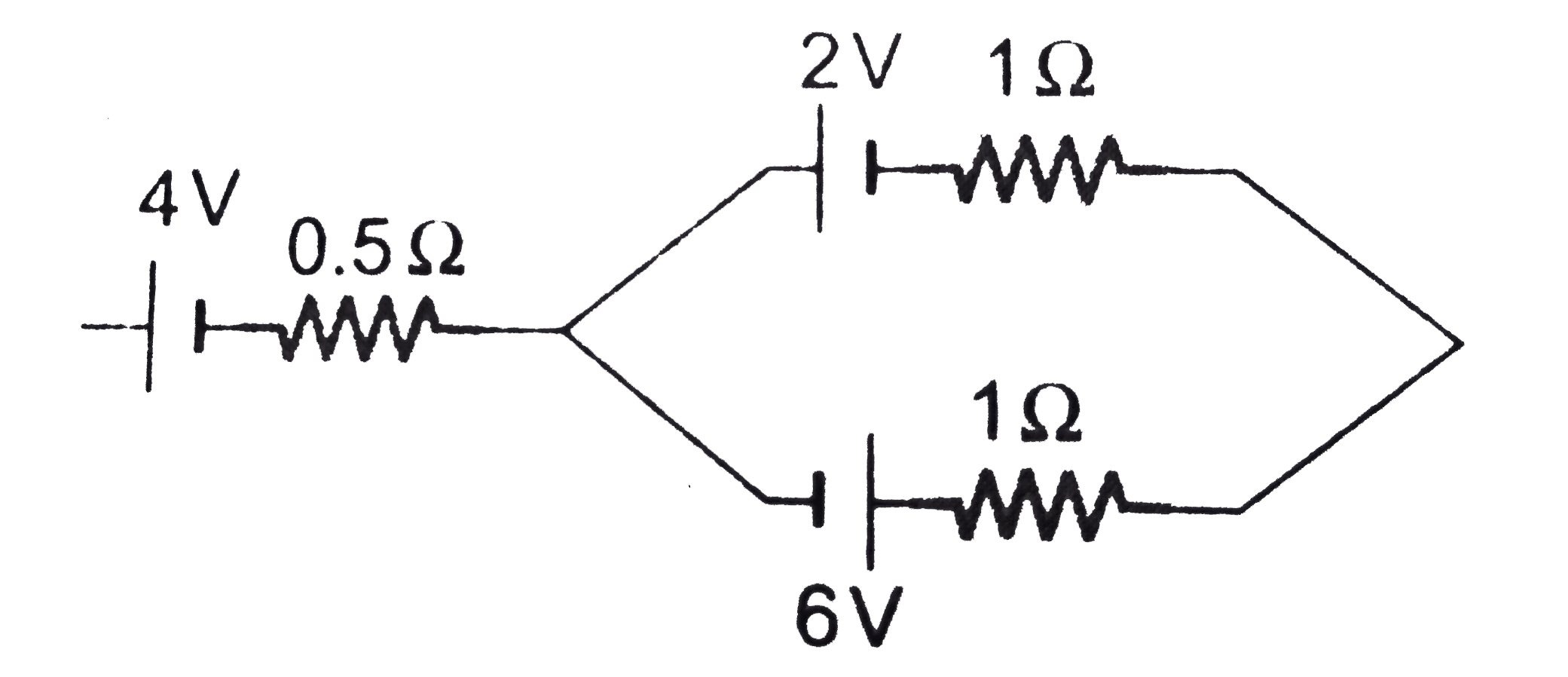
Find the emf and internal resistance of a single battery which is equivalent to a combination of three batteries as show in figure.
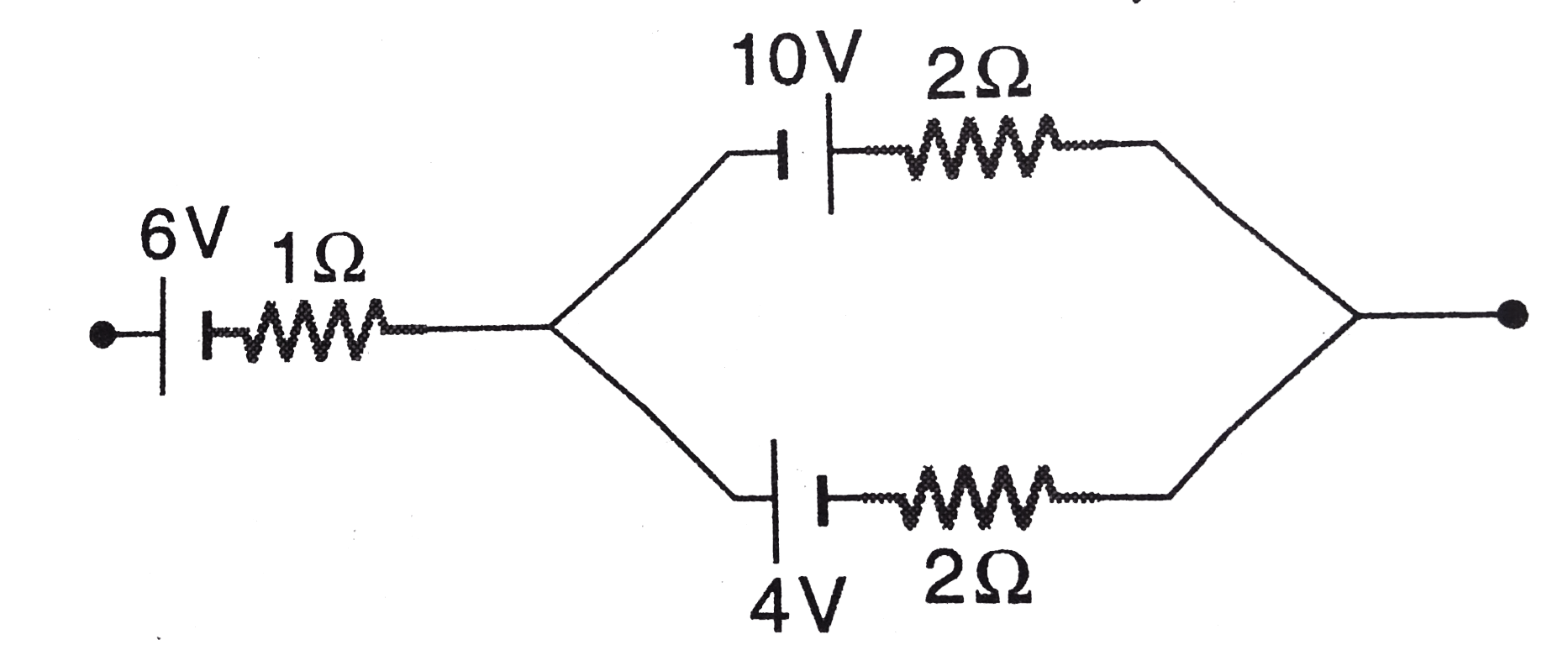
The given combination consists of two batteries in parallel and resultant of these two in series with the third one.
For parallel combination we can apply.
Eeq=E1r1−E2r21r1+1r2=102−4212+12=3V
Further, 1req=1r1=1r2=12+12=1
=∴req=1Ω
Now this is in series with find one i.e.

The equivalent emf of these two is (6−30Vor3V) and the internal resistance will be (11) or 2Ω

Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - DC PANDEYCHAPTER - CURRENT ELECTRICITYEXERCISE - Example Type 1
2 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEYCHAPTER - CURRENT ELECTRICITYEXERCISE - Example Type 2
1 Videos
- COMMUNICATION SYSTEMBOOK - DC PANDEYCHAPTER - COMMUNICATION SYSTEMEXERCISE - Subjective
11 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEYCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Medical entrances gallery
25 Videos
Similar Questions
Find the emf (V) and internal resistance (R) of a single battery which is equivalent toa parallel combination of two batteries of emf V1 and V2 and internal resistances r1 and r2 respectively, with polrities as shown in figure
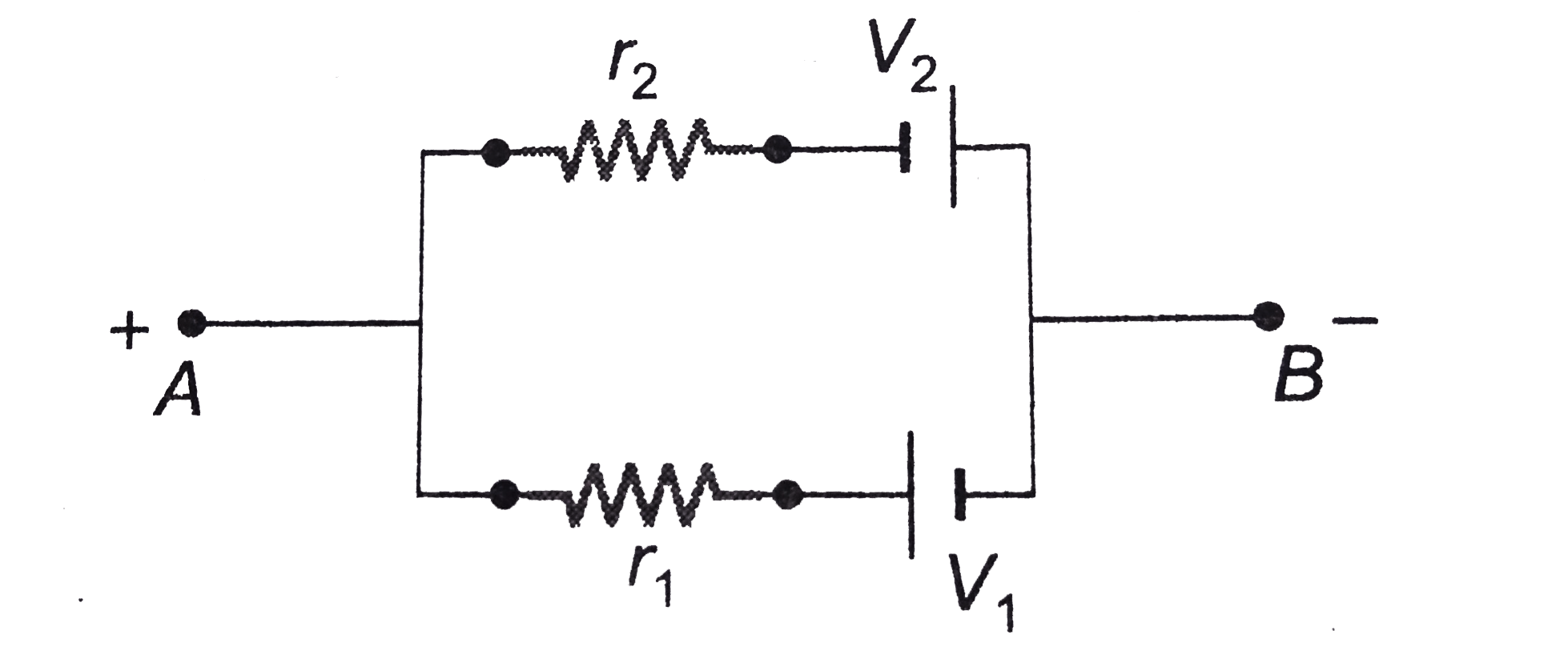
View SolutionFind the emf (V) and internal resistance (r) of a single battery which is equivalent to a parallel combination of two batteries of emf's V1,andV_(2), and internal resistance r1 and r2 respectively, with polarities as shown in the figure
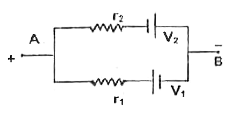
View Solution
Knowledge Check
The emf of the battery shown in figure is
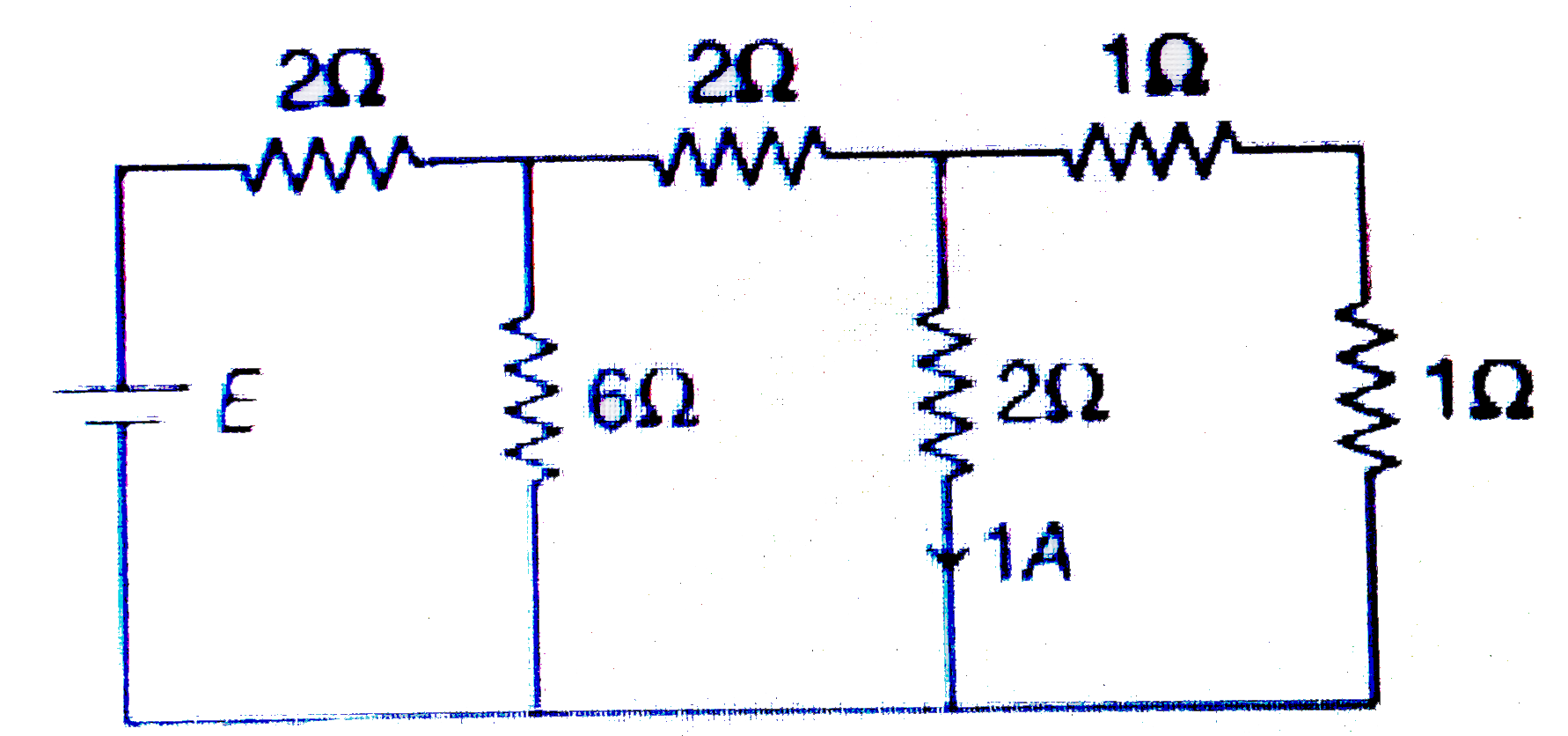 A12 VB16 VC18 VD15 V
A12 VB16 VC18 VD15 V
Find the e.m.f(E0) end internal resistance (r0) of a simple battery which is equivalent to a perallel combination of two battery of e.m.fE1andE2 and internal resistance v1andv2 respectively with polarities
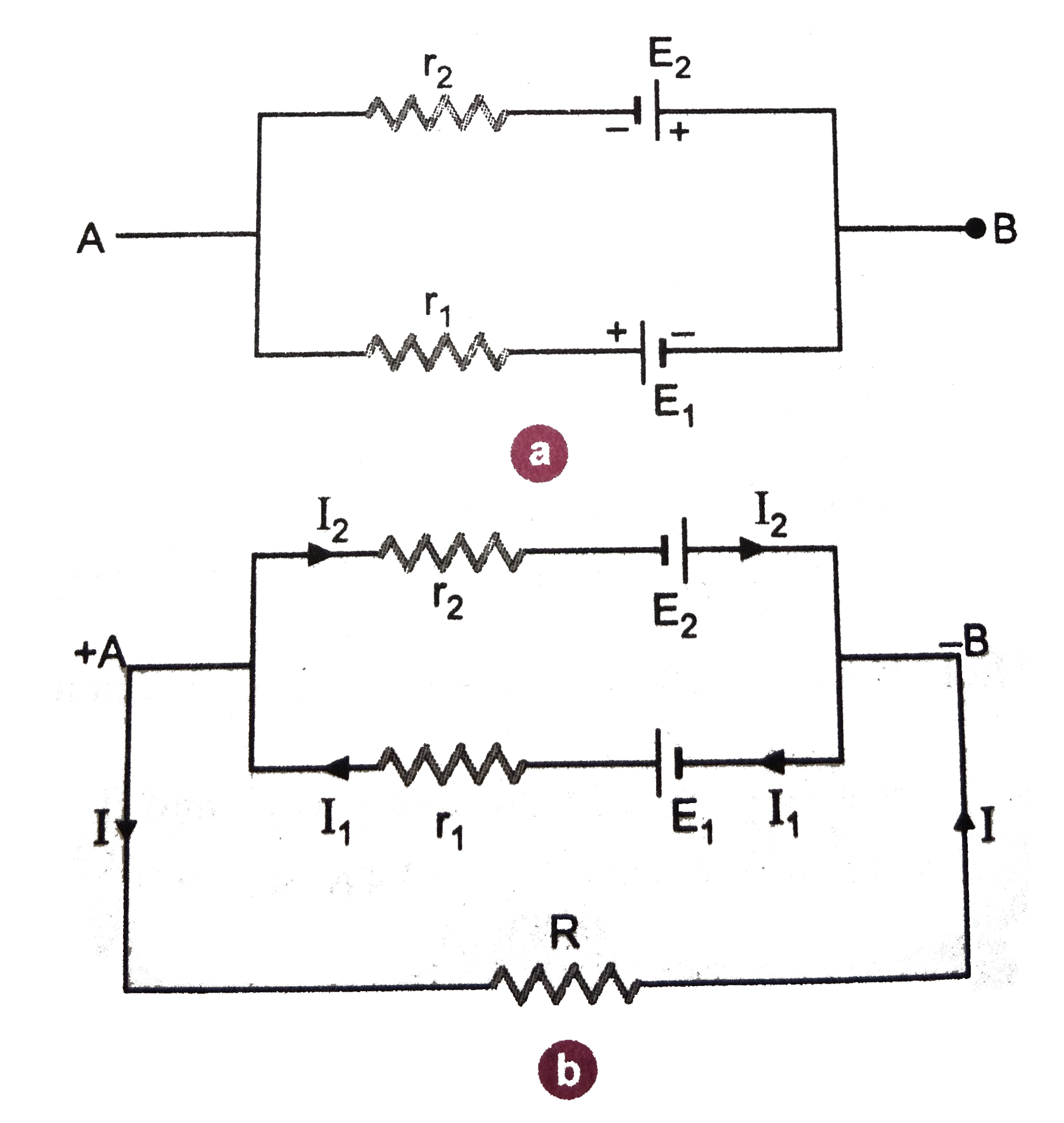
View Solution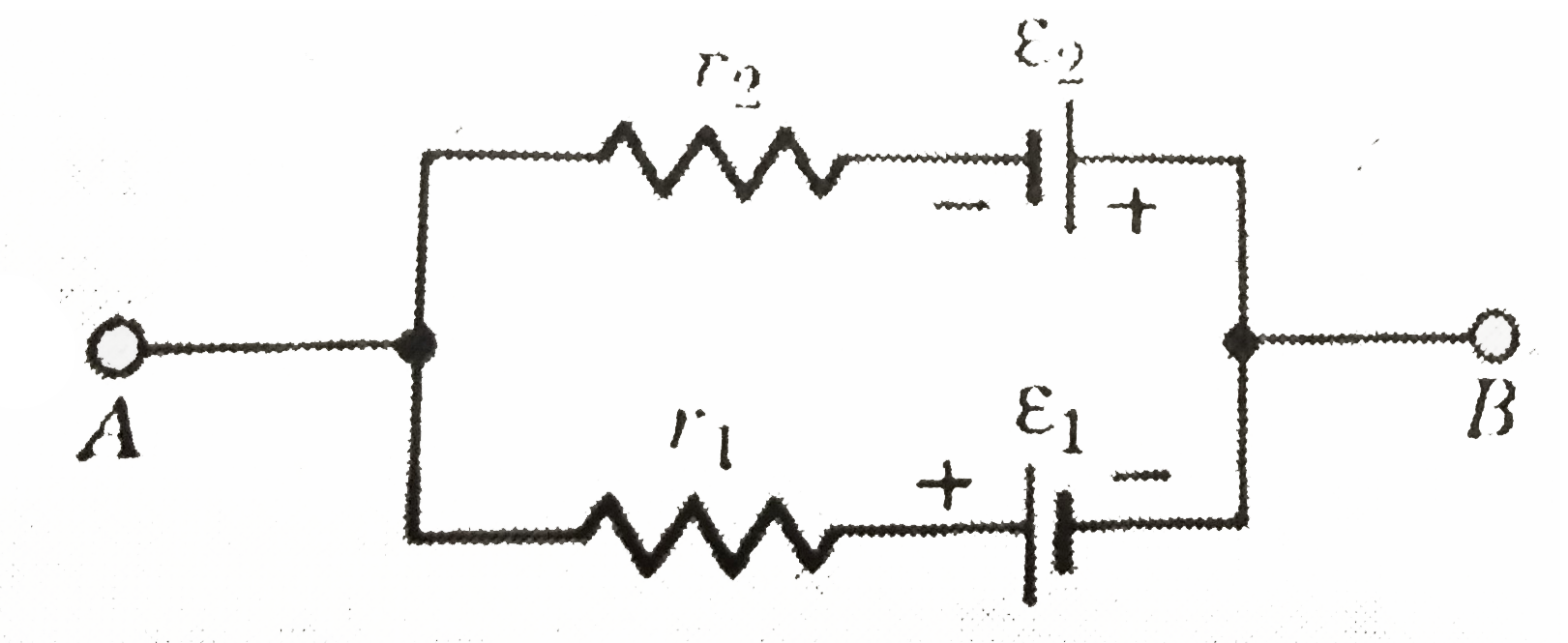
find the emf (ε0) and internal resistance (r0) if a battery which is equivalent to a parallel combination of two batteries of emfs ε1andε2 and internal resistances r1andr2 respectively, with polarities as shown in figure.
View SolutionFind the net emf of the three batteries shown in figure
View SolutionFind the emf and the internal resistance of a source which is equivalent to two batteries connected in parallel whose emf's are equal to E1 and E2 and internal resistances to R1 and R2
View SolutionFind the emf ε and the internal resistance r of an electric source which is equivalent to two batteries of emf's ε1 and ε2 and internal resistances r1andr2, connected in parallel.
View SolutionTwo batteries of emf 12V and 6V and internal resistance 2Ω and 1Ω are connected in parallel and the combination is connected to a resisor of 2Ω through a key. Find the potential difference between the positive and negative terminals of the batteries (a) When key is open, b) when key is closed. Find the emf and internal resistance of a single cell which would be equivalent to the combination.
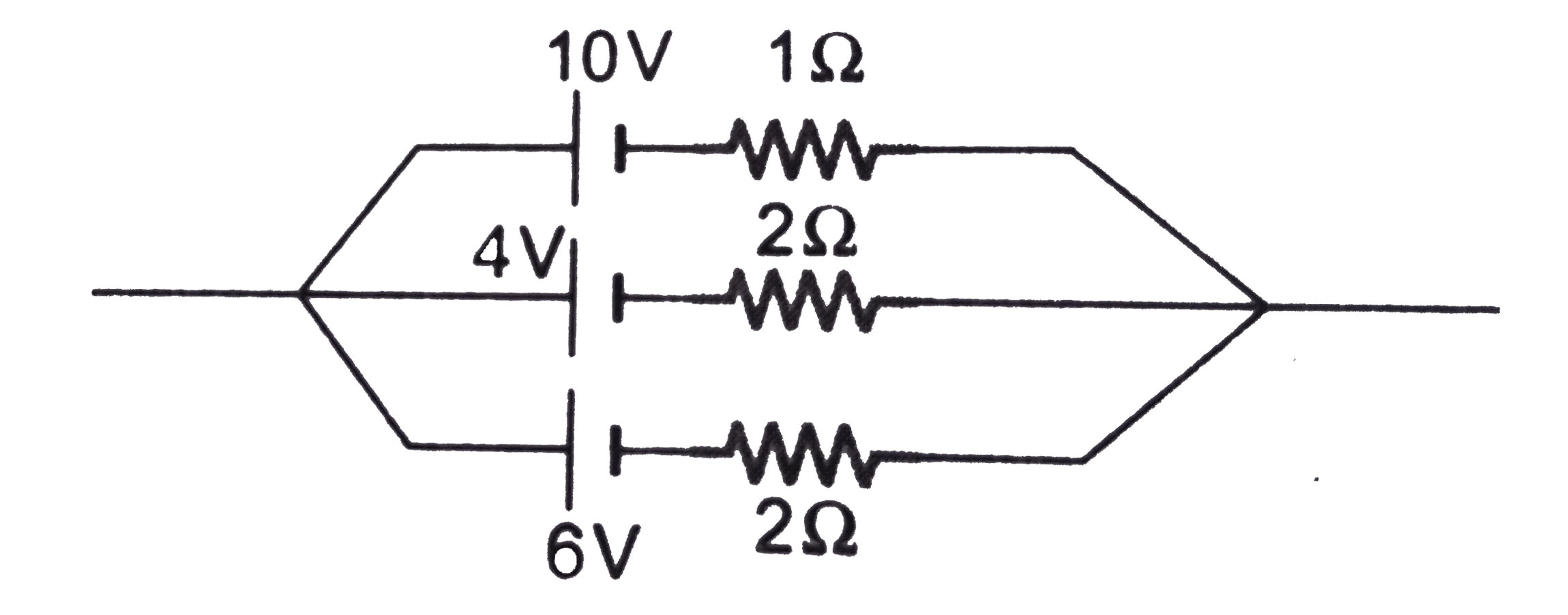
View SolutionFind the equivalent emf and internal resistance of the arrangement shown in figure.
View Solution
