If ABCD is a parallelogram, the prove that ar(ABD)=ar(BCD)=ar(ABC)=ar(ACD)=1/2a r(∣∣gmA B C D)
Given:ABCD is a parallelogram.
When we join the diagonal of parallelogram, it divides it into two quadrilaterals.
Proof:
Let AC is the diagonal, then
ar(ΔABC)=ar(ΔACD)=12ar(ABCD)
Let BD be another diagonal
ar(ΔABD)=ar(ΔBCD)=12ar(ABCD)
Now, we have
ar(ΔABC)=ar(ΔACD)
=ar(ΔABD)=ar(ΔBCD)
=12ar(ABCD)
Hence Proved.
Topper's Solved these Questions
Similar Questions
If ABCD is a parallelogram, then prove that ar(△ABD)=ar(△BCD)=ar(△ABC)=ar(△ACD)=12ar(∣∣gmABCD)
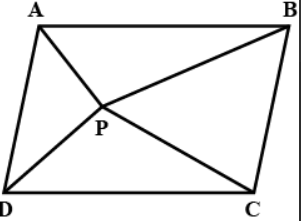
View SolutionIn Figure, P is a point in the interior of a parallelogram ABCD. Show that ar(APB)+ar(PCD)=12ar (||gmABCD) ar (APD)+ar (PBC)=ar (APB)+ar(PCD)

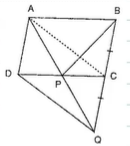
View SolutionIn Figure, ABCD is a parallelogram. Prove that: ar(BCP)=ar(DPQ) CONSTRUCTION : Join AC.
View SolutionIn Figure, P is a point in the interior of a parallelogram ABCD . Show that ar(APB)+ar(PCD)=12ar(^(gm)ABCD) aR(APD)+ar(PBC)=ar(APB)+ar(PCD)
View SolutionABCD is a parallelogram X and Y are the mid-points of BC and CD respectively. Prove that ar(AXY)=38ar(∣∣gmABCD)
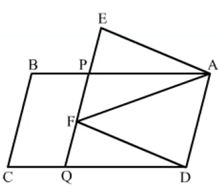
View SolutionIn Figure, ABCDandAEFD are two parallelograms? Prove that: ar(APE):ar(PFA)=ar(QFD):ar(PFD)
View SolutionABCD IS A PARALLELOGRAM AND O is any point in its interior. Prove that: ar (AOB)+ ar (COD)= ar (BOC)+ ar(AOD) ar (AOB)+ar (COD)=12 ar(^(gm)ABCD) Given: A parallelogram ABCD and O is a point in its interior. To Prove: ar ( AOB)+ ar(COD)=ar (BOC)+ar(AOD)
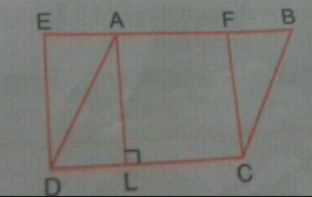
View SolutionIn Figure, ABCD is a parallelogram and EFCD is a rectangle. Also AL⊥DC. Prove that : ar(ABCD)=ar(EFCD) ar(ABCD)=DC×AL

View SolutionThe mid points of the sides of a triangle ABC along with any of the vertices as the fourth point make a parallelogram of area equal to:
(a)ar (ABC) (b) 12ar (ABC) 13ar (ABC) (d) 14 ar (ABC)
View SolutionIn the following figure, ABCD is a parallelogram and EFCD is a rectangle. Also, AL⊥DC. Prove that
(i) ar(ABCD)=ar(EFCD)
(ii) ar(ABCD)=DC×AL.
View Solution