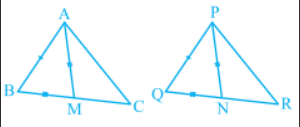
Triangles having equal areas and having one side of one of the triangles, equal to one side of the other, have their corresponding altitudes equal. GIVEN : Two triangles $A B C$ and $P Q R$ such that: $a r (A B C) = A R (P Q R)$ (ii) $A B = P Q$

Video Solution

Text Solution

Verified by Experts

Given : Two triangles $A B C$ and $P Q R$ such that (i) $a r (Δ A B C) = a r (Δ P Q R)$ and (ii) $A B = P Q$ .
$C N$ and $R T$ and the altitude corresponding to $A B$ and $P Q$ respectively of the two triangles.
To prove: $C R = R T$
Proof: In $Δ A B C$ ,
$C N$ is the altitude corresponding to the side AB.
$a r (Δ A B C) = \frac{1}{2} A B \times C N$ ....(i)
Similarly, $a r (Δ P Q R) = \frac{1}{2} P Q \times R T$ ....(ii)
From equation (i) and (ii), we get:
$a r (Δ A B C) = a r (Δ P Q R)$ [Given]
$∴ \frac{1}{2} A B \times C N = \frac{1}{2} P Q \times R T$
Also, $A B = P Q$ [Given]
$C N = R T$
Hence proved.

Updated on:21/07/2023

If in two right triangles, the hypotenuse and one side of one triangle are equal to the hypotenuse and one side of the other triangle, then the two triangles are congruent. 1.
PL is an altitude from P of $Δ P Q R$ on QR such that QL = LR. Then,
A $∠ Q < ∠ R$
B $∠ Q = ∠ R$
C $∠ Q > ∠ R$
D $∠ P = ∠ R$
${(p \land (p \to q)) \land (q \to r)} \to r$ is equal to
A $q \to ~ r$
B $p \to ~ r$
Cfallacy
Dtautology