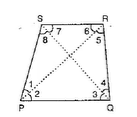
PQRS is a square. PR and SQ intersect at O. State the measure of ∠POQ.
∠SPQ=90∘
∠QPO=12∠QPS=45∘
∠PQD=45∘
In∠QPO
∠OPQ+∠PQO+∠QOP+∠PQO=180∘
45+45+∠QOP=180
∠QOP=90∘.
Topper's Solved these Questions
Similar Questions
Knowledge Check
If the sum of the square of p and twice of q is equal to the square root of the sum of the square of r and s, wirte a formula wth p as the subject.
Ap=√2p−√r2+s2Bp=√r2+s2−2qCp=√2q−r2−s2Dp=√1−k2
ABCD is a parallelogram whose AC and BD intersect at O. A line through O intersects AB at P and DC at Q. Prove that ar ( POA)= ar ( QOC).
View SolutionABCD is a parallelogram whose diagonals AC and BD intersect at O. A Line through O intersects AB at P and DC at Q. Prove that ar(△POA)=ar(△QOC).
View SolutionIn Figure, PQRS is a quadrilateral. PQ is its longest side and RS is its shortest side. Prove that ∠R> ∠P and ∠S> ∠Q Given : PQRS is a quadrilateral. PQ is its longest side and RS is its shortest side. To Prove : (i) ∠R> ∠P (ii) ∠S> ∠Q Construction : Joint PR and QS
View SolutionIn Fig. 4.238, S and T are points on the sides PQ and PR respectively of PQR such that PT=2cm , TR=4cm and ST is parallel to QR . Find the ratio of the areas of PST and PQR . (FIGURE)
View SolutionPQRS is a rectangle inscribed in a quadrant of a circle of radius 13cm. A is any point on PQ. If PS=5cm, then find ar(RAS)
View SolutionThe diagonals of a parallelogram ABCD intersect at a point O. Through O, a line is drawn to intersect AD at P and BC at Q. Show that PQ divides the parallelogram into two parts of equal area.
View SolutionIn Fig. 6.44, the side QR of PQR is produced to a point S. If the bisectors of ∠PQR and ∠PRS meet at point T, then prove that ∠QTR=12∠QPR.

View Solution
