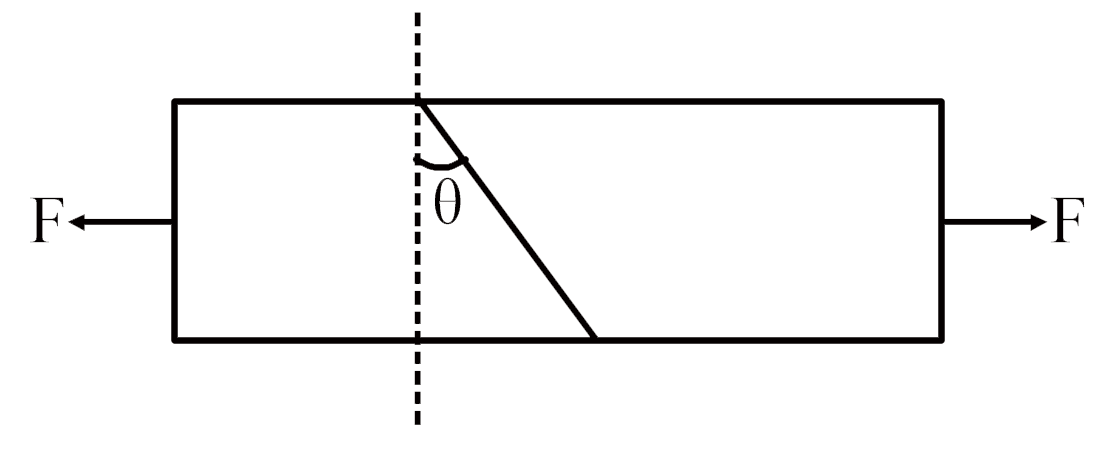
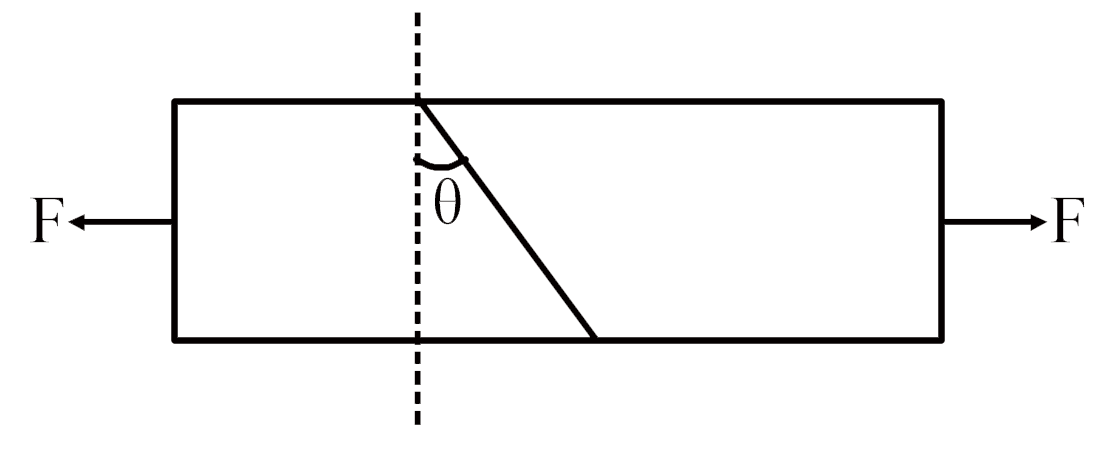
Consider a long steel bar under a tensile stress due to forces F, acting at the edges along the length of the bar

Consider a plane making an angle θ with the length. What are the tensile and shering stresses on this plane ? (a) For what angle is the tensile stress a maximum ? (b) For what angle is the shearing stress a maximum ?
Consider the adjacent diagram.
Let the cross-sectional area of the bar be A. Consider the equilibrium of the plane aa'. A force F must be acting on this plane making an angle π2−θ with the normal ON. Resolving F into components, along the plane (FP) and normal to the plane.
FP=Fcosθ
FN=Fsinθ
Let the area of the face aa' be A', then
AA'=sinθ
∴ A'=Asinθ
The tensile stress = Normal forceArea=FsinθA'
=FcosθA/sinθ=FAsinθ.cosθ
Shearing stress = Parallel forceArea
=FcosθA/Sinθ=FAsinθ.cosθ
=F2A(2sinθ.cosθ)=F2Asin2θ
(a) For tensile stress to be maximum, sin2θ=1
⇒ sinθ=1
⇒ θ=π2
(b) For shearing stress to be maximum,
sin2θ=1
⇒ 2θ=π2
⇒ θ=π4
Note We must not apply the formula for stress directly, forces must be resolved.

Topper's Solved these Questions
- MECHANICAL PROPERTIES OF SOLIDSBook:NCERT EXEMPLARChapter:MECHANICAL PROPERTIES OF SOLIDSExercise:LONG SHORT ANSWER TYPE QUESTION
Explore 16 Videos
- MECHANICAL PROPERTIES OF FLUIDSBook:NCERT EXEMPLARChapter:MECHANICAL PROPERTIES OF FLUIDSExercise:Long Answer Type Questions
Explore 3 Videos
- MOTION IN A PLANEBook:NCERT EXEMPLARChapter:MOTION IN A PLANEExercise:Multiple Choice Questions
Explore 37 Videos
Similar Questions
A bar of cross-section A is subjected two equal and opposite tensile forces at its ends consider a plane section of the bar whose makes an angle θ with the axis of the bar.
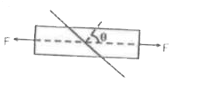
(a) what is the tensile stress on this plane ?
(b)what is the shearing stress on this plane ?
(c )for what value of θ is the tensile stress is maximum ?
(d) for what value of θ is the shearing stress maximum ?
View SolutionA bar of cross section A is subjected to equal and opposite tensile force at its ends. Consider a plane section of the bar whose normal makes an angle θ with the axis of the bar.

a. What is the tensile stress on the plane?
b. What is the shearing stress on the this plane?
c. For what value of θ is the tensile stress maximum?
d. For what value of θ is the shearing stress maximum?
View Solution
Knowledge Check
Consider a long steel bar under a tensille due to force F acting at the edges along the length of the bar (figure). Consider a plane making an angle θ with the length. For what angle is the tensile stress a maximum?
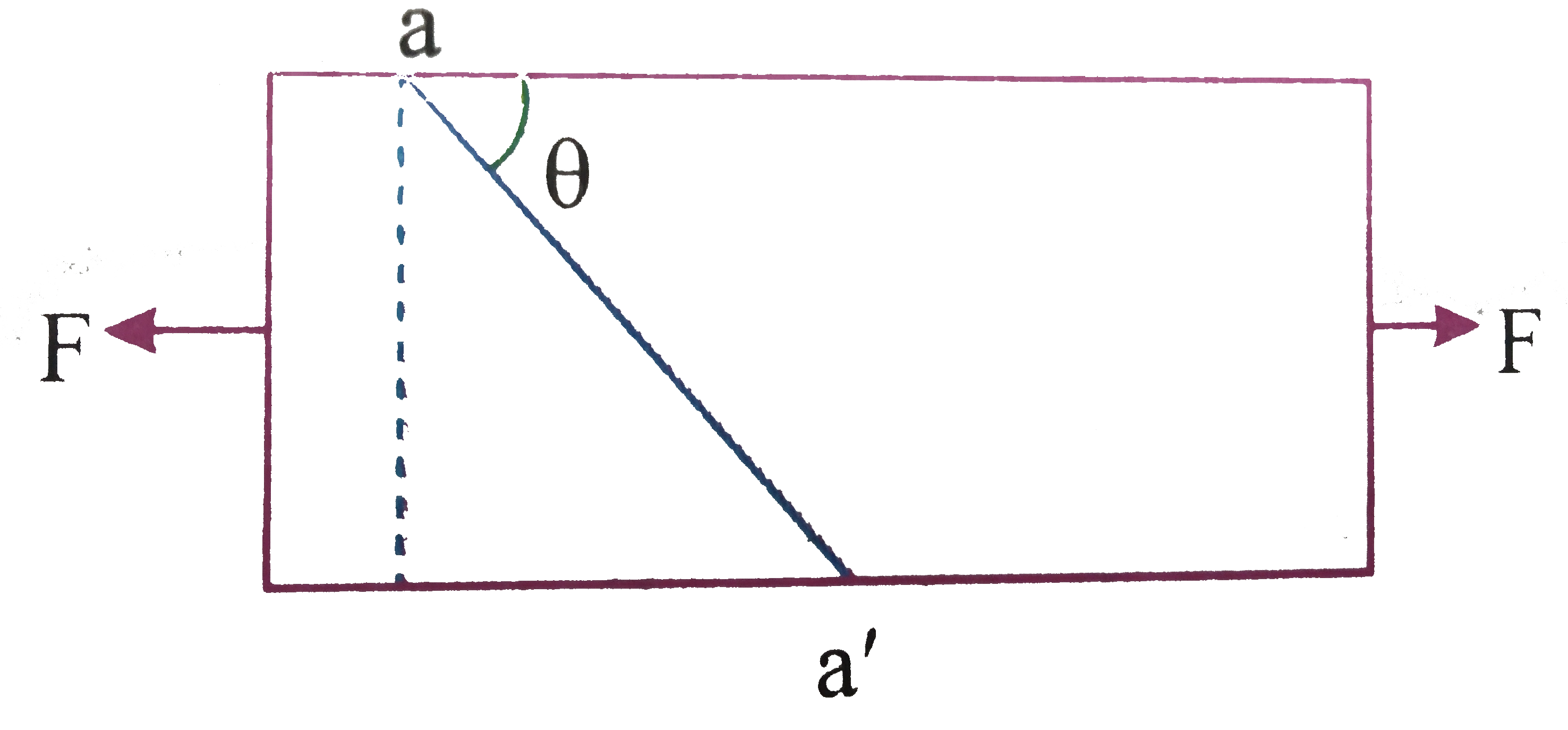 A30∘B45∘C60∘D90∘
A30∘B45∘C60∘D90∘In the above problem, for what angle is the shearing stress a maximum?
A30∘B45∘C60∘D90∘In the question rumber 66, for what value of θ, shearing stress is maximum?
A0∘B30∘C45∘D90∘
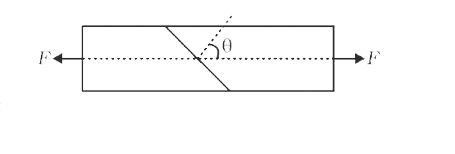
A bar of cross-section A is subjected to equal and opposite tensile forces at its ends. Consider a plane section of the bar whose normal makes an angle θ with the axis of the bar .
(i) What is the tensile stress on this plane?
(ii) What is the shearing stress on this plane?
(iii) For what value of θ is the tensile stress maximum
(iv) For what value of θ is the shearing stress maximum?
View SolutionA bar of cross section A is subjected to equal and opposite tensile forces F at its ends. Consider a plane through the bar making an angle θ with a plane at right angles to the bar as shown in figure.

In the above problem, for what value of θ is the tensile stress maximum ?
View SolutionA bar of cross section A is subjected to equal and opposite tensile forces F at its ends. Consider a plane through the bar making an angle θ with a plane at right angles to the bar as shown in figure.
The tensile stress at this plane in terms of F, A and θ is
View SolutionA bar of cross section A is subjected to equal and opposite tensile forces F at its ends. Consider a plane through the bar making an angle θ with a plane at right angles to the bar as shown in figure.
The shearing stress at the plane, in terms of F, A and θ is
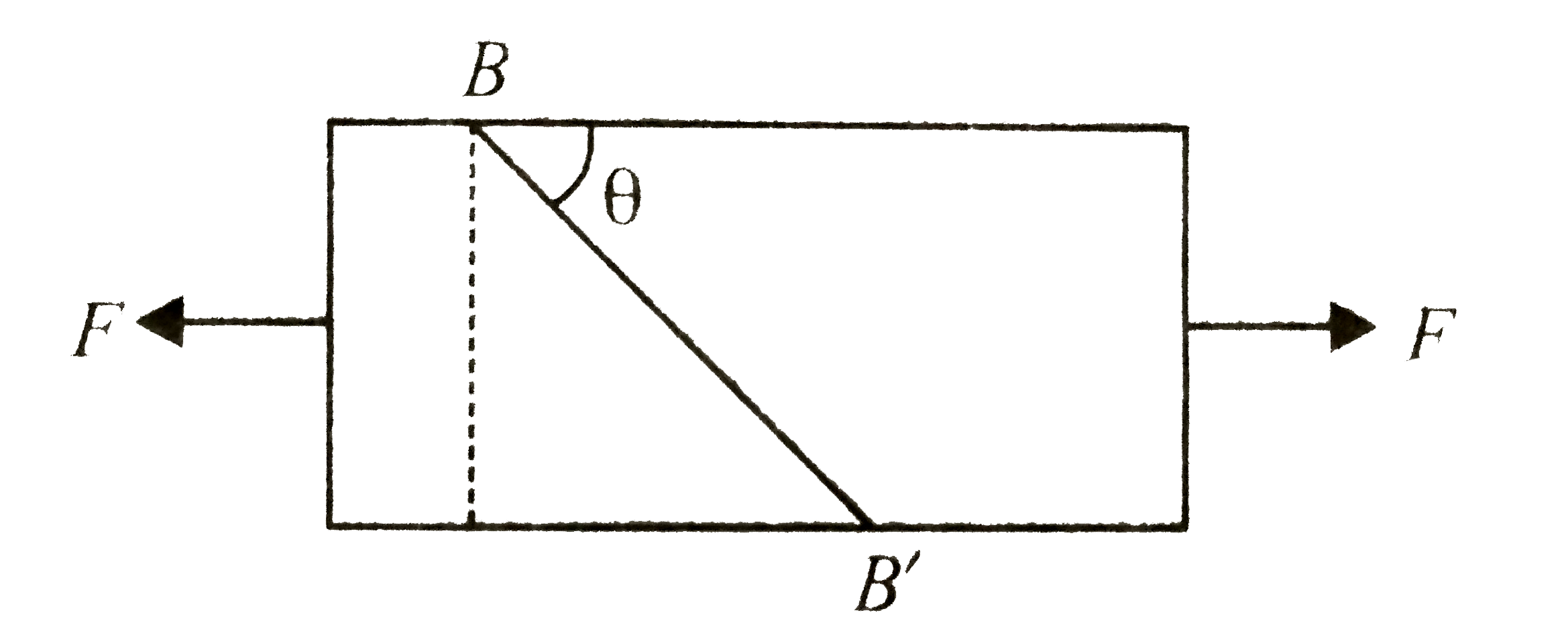
View SolutionA bar of cross- sectional area A is is subjected two equal and opposite tensile forces at its ends as shown in figure. Consider a plane BB' making an angle θ with length
View Solution

