A bar of cross- sectional area A is is subjected two equal and opposite tensile forces at its ends as shown in figure. Consider a plane BB' making an angle with length
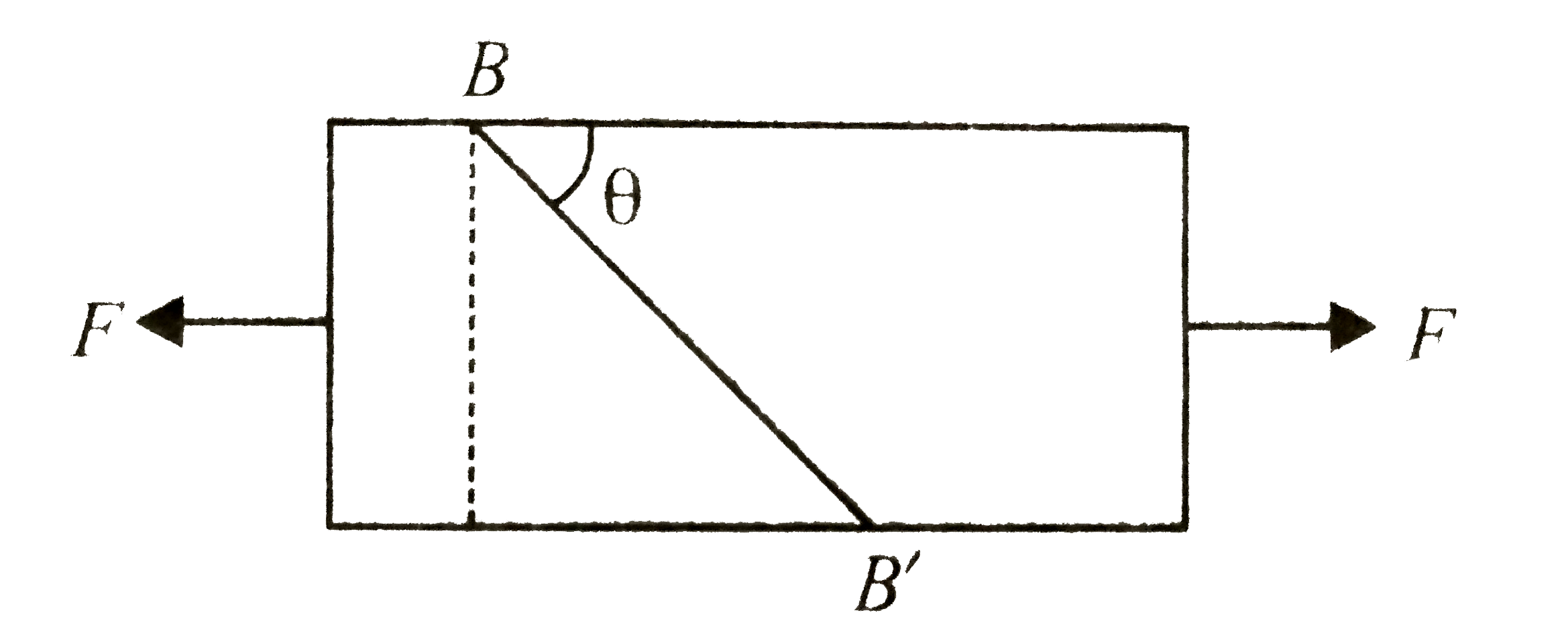
The correct Answer is:A
Consider the equilibrium of the palne BB.
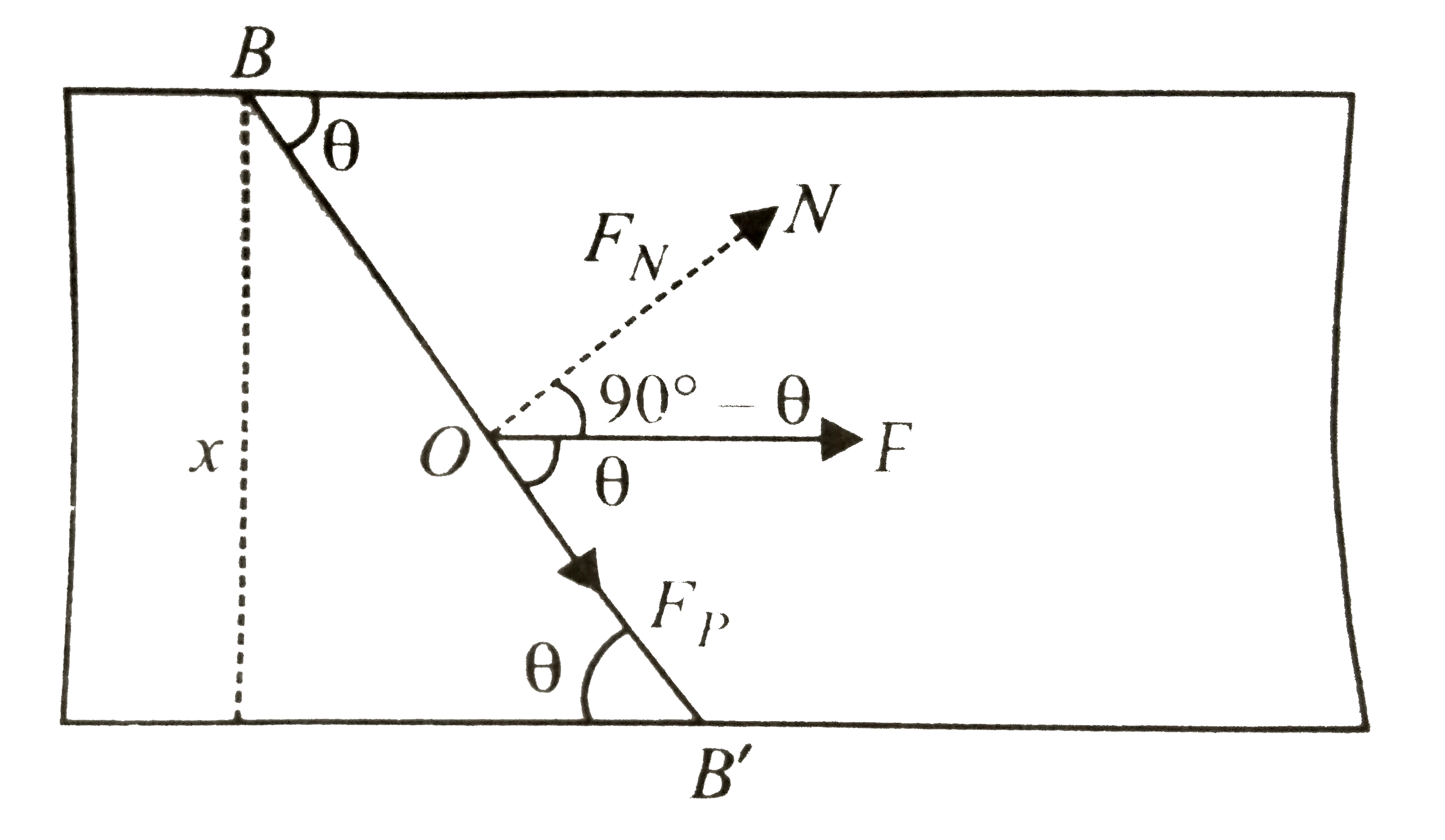
A force F must be acting on this on this plane making an angle with the normal ON. Resolving F into two components, along the palne and normal to the plane.
Component of force F along the palne, Component of force F normal to the palne ,
Let the are of the face BB be A . Then
Tensile strss
Shearing stress
Their corresponding ratio is
Topper's Solved these Questions
- MECHANICAL PROPERTIES OF SOLIDSBOOK - NCERT FINGERTIPSCHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - Applications Of Elastic Behaviour Of Materials
8 Videos
- MECHANICAL PROPERTIES OF SOLIDSBOOK - NCERT FINGERTIPSCHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - Higher Order Thinking Skills
8 Videos
- MECHANICAL PROPERTIES OF SOLIDSBOOK - NCERT FINGERTIPSCHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - Stress-Strain Curve
5 Videos
- MECHANICAL PROPERTIES OF FLUIDSBOOK - NCERT FINGERTIPSCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - Assertion And Reason
15 Videos
- MOTION IN A PLANE BOOK - NCERT FINGERTIPSCHAPTER - MOTION IN A PLANE EXERCISE - Assertion And Reason
15 Videos
Similar Questions
A bar of cross section A is subjected to equal and opposite tensile forces F at its ends. Consider a plane through the bar making an angle θ with a plane at right angles to the bar as shown in figure.
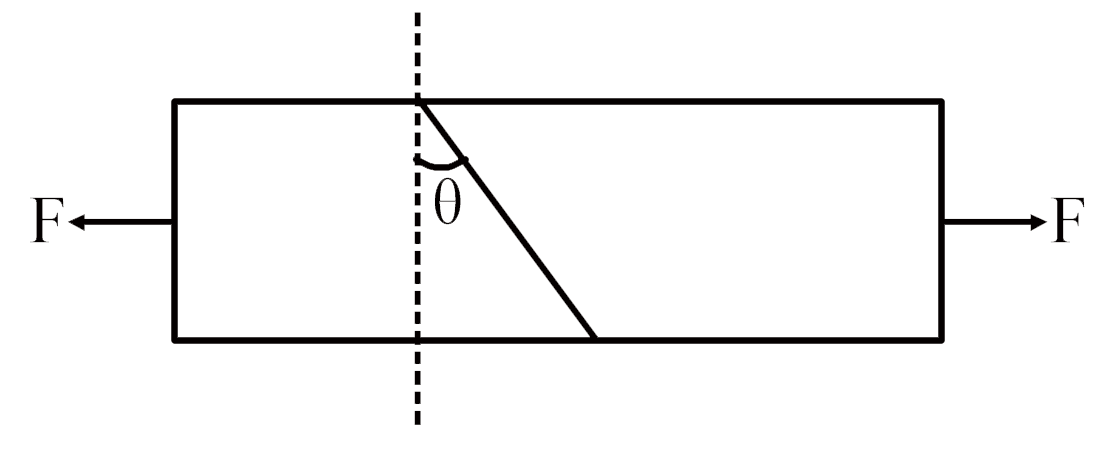
The tensile stress at this plane in terms of F, A and θ is
View SolutionA bar of cross section A is subjected to equal and opposite tensile forces F at its ends. Consider a plane through the bar making an angle θ with a plane at right angles to the bar as shown in figure.

In the above problem, for what value of θ is the tensile stress maximum ?
View SolutionA bar of cross section A is subjected to equal and opposite tensile forces F at its ends. Consider a plane through the bar making an angle θ with a plane at right angles to the bar as shown in figure.
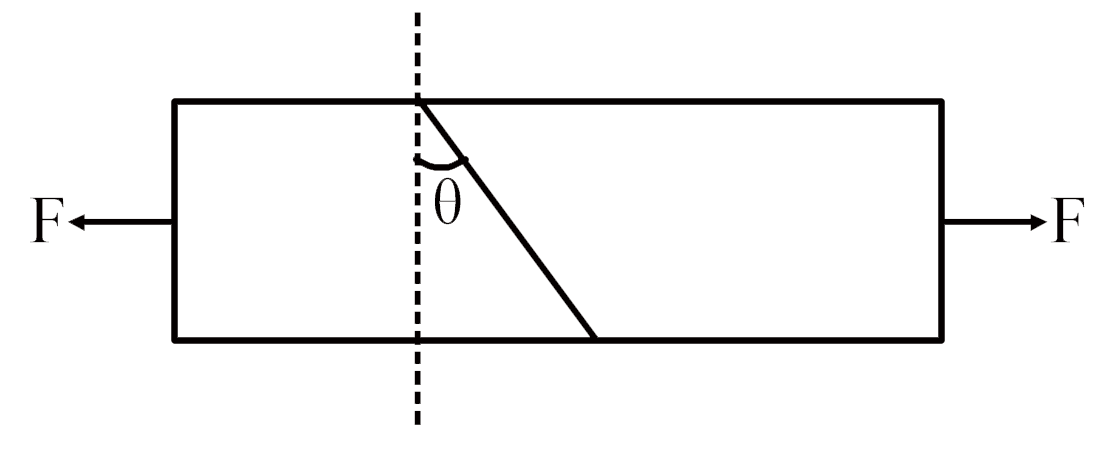
The shearing stress at the plane, in terms of F, A and θ is
View SolutionA bar of cross-section A is subjected two equal and opposite tensile forces at its ends consider a plane section of the bar whose makes an angle θ with the axis of the bar.
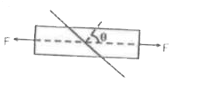
(a) what is the tensile stress on this plane ?
(b)what is the shearing stress on this plane ?
(c )for what value of θ is the tensile stress is maximum ?
(d) for what value of θ is the shearing stress maximum ?
View SolutionA bar of cross-section A is subjected to equal and opposite tensile forces at its ends. Consider a plane section of the bar whose normal makes an angle θ with the axis of the bar .
(i) What is the tensile stress on this plane?
(ii) What is the shearing stress on this plane?
(iii) For what value of θ is the tensile stress maximum
(iv) For what value of θ is the shearing stress maximum?
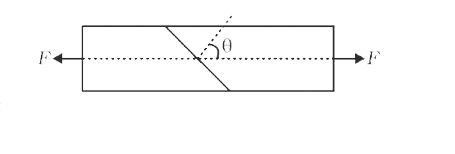
View SolutionA bar of cross section A is subjected to equal and opposite tensile force at its ends. Consider a plane section of the bar whose normal makes an angle θ with the axis of the bar.

a. What is the tensile stress on the plane?
b. What is the shearing stress on the this plane?
c. For what value of θ is the tensile stress maximum?
d. For what value of θ is the shearing stress maximum?
View SolutionA steel bar of cross section A is subjected to two equal and opposite pulling forces at the two ends. If there is a plane through the bar making an angle α as shown, find

the shearing stress at this plane
View SolutionA steel bar of cross section A is subjected to two equal and opposite pulling forces at the two ends. If there is a plane through the bar making an angle α as shown, find

for what α the shearing strain is maximum.
View SolutionA rod area of cross section A is being acted upon by two forces F - F as shown in figure. Consider a section ab of rod whose normal makes angle θ with horimontal. The shear stress upon this section is maximum when θ=180∘n. Find n.

View SolutionFig shows a bar of uniform cross section of area s. Equal and opposite tensile forces are applied at the ends of the bar. Each force has a magnitude F. ABCD is a plane trough the bar and inclined at angle θ with the perpendicular to the length of the bar.

Normal stress at the plane which is inclined with the plane perpendicular to the length of the bar is -
View Solution
