(a) Pressure decreases as one ascends the atmosphere. If the density of air is $ρ,$ What is the change in pressure dp over a differential height dh ? (b) Considering the pressure p to be proportional to the density, find the pressure p at a height h if the pressure on the sureface of the earth is $p_{0} .$ (c ) If $p_{0} = 1.03 \times 10^{5} N m^{- 2}, ρ_{0} = 1.29 k g m^{- 3} and g = 9.8 m s^{- 2},$ at what height will the pressure drop to $(1 / 10)$ the value at the surface of the earth ? (d) This model of the atmosphere works for relatively small distance. Identify the underlying assumption that limits the model.

Video Solution

Text Solution

Verified by Experts

Consider a horizontal parcel of air with cross-section A and height dh.

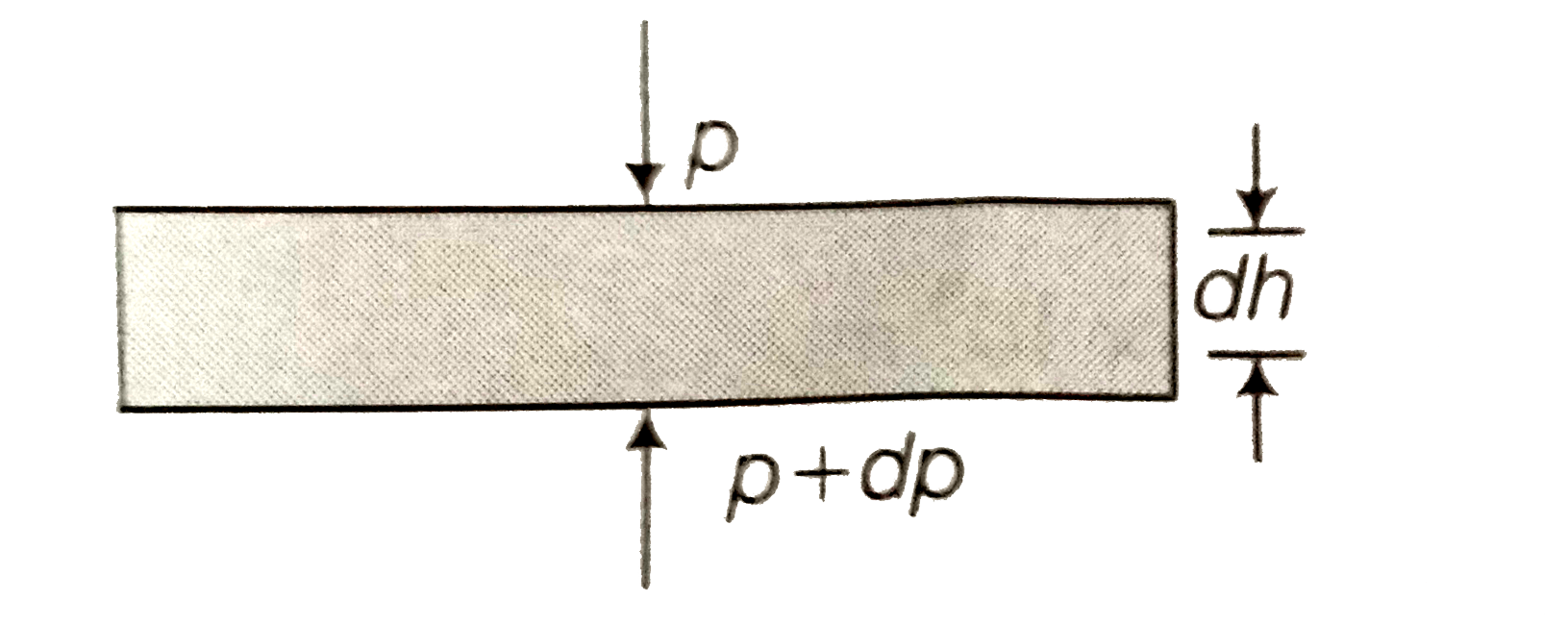
Let the pressure on the top surface and bottom surface be p and p+ dp. If the parcel is in equilibrium , then the net upward force must be balanced by the weight.
i.e., $(p + d p) A - p A = - ρ g A d h (∵$ weight =Density $\times$ Volume $\times g)$
$= - ρ \times A d h \times g$
$\Rightarrow d p = - ρ g d h . (ρ =$ density of air $)$
Negative sign shows that pressure decreases with height .
(b) Let $p_{\circ}$ be the density of air on the surface of the earth.
As per question, pressure $\propto$ density
$\Rightarrow \frac{p}{p_{\circ}} = \frac{ρ}{ρ_{\circ}}$
$\Rightarrow ρ = \frac{ρ_{\circ}}{p_{\circ}} p d h [∵ d p = - ρ g d h]$
$\Rightarrow \frac{d p}{p} = - \frac{ρ_{\circ} g}{p_{\circ}} d h$
$\Rightarrow p \int p_{\circ} \frac{d p}{p} = - \frac{ρ_{\circ} g}{p_{\circ}} h \int 0 d h [\begin{matrix} ∵ at h = 0 & r = p_{\circ} and at h = h & p = p \end{matrix}]$
$\Rightarrow In \frac{p}{p_{\circ}} = - \frac{ρ_{\circ} g}{p_{\circ}} h$
By removing log, $p = p_{\circ} e (- \frac{ρ_{\circ} g h}{p_{\circ}})$
(c) As $p = p_{\circ} e^{- \frac{ρ_{\circ} g h}{p_{\circ}}}$ ,
$\Rightarrow In \frac{p}{p_{\circ}} = - \frac{ρ_{\circ} g h}{P_{\circ}}$
By question,
$p = \frac{1}{10} p_{\circ}$
$\Rightarrow In ⎛ ⎝ \frac{\frac{1}{10} p_{\circ}}{p_{\circ}} ⎞ ⎠ = - \frac{ρ_{\circ} g}{p_{\circ}} h$
$\Rightarrow In \frac{1}{10} = - \frac{ρ_{\circ} g}{p_{\circ}} h ρ_{\circ}$
$h = - \frac{p_{\circ}}{ρ_{\circ} g} In \frac{1}{10} = - \frac{p_{\circ}}{p_{\circ} g} In {(10)}^{- 1} = \frac{p_{\circ}}{p_{\circ} g} In 10$
$= \frac{p_{\circ}}{ρ_{\circ} g} \times 2.303$ [ $∵$ In $(x) = 2.303 {log}_{10} (x)]$
$= \frac{1.013 \times 10^{5}}{1.22 \times 9.8} \times 2.303 = 0.16 \times 10^{5}$ m
$= 16 \times 10^{3}$ m
(d) We know that $p \propto ρ$ (when T=constant i.e., isothermal pressure)
Temperature (T) remains constant only near the surface of the earth , not at greater heights.

Updated on:21/07/2023

The pressure at depth h below the surface of a liquid of density $ρ$ open to the atmosphere is
Agreater than the atmospheric pressure by $ρ g h$
Bless than the atmospheric pressure by $ρ g h$
Cequal to the atmospheric pressure
Dincreases exponentially with depth
It P is the pressure and $ρ$ is the density of a gas, then P and $ρ$ are realted as :
A $P \propto ρ$
B $P \propto ρ^{2}$
C $P \propto 1 / ρ$
D $P \propto 1 / ρ^{2}$
If $P$ is the pressure of a gas and $ρ$ is its density , then find the dimension of velocity in terms of $P$ and $ρ$ .
A $P^{1 / 2} ρ^{- 1 / 2}$
B $P^{1 / 2} ρ^{1 / 2}$
C $P^{- 1 / 2} ρ^{- 1 / 2}$
D $P^{- 1 / 2} ρ^{- 1 / 2}$