A bar of cross-section A is subjected two equal and opposite tensile forces at its ends consider a plane section of the bar whose makes an angle θ with the axis of the bar.
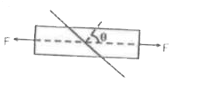
(a) what is the tensile stress on this plane ?
(b)what is the shearing stress on this plane ?
(c )for what value of θ is the tensile stress is maximum ?
(d) for what value of θ is the shearing stress maximum ?
The resolved part of F along the normal is the tensile force on this plane and the resolved part parallel to the plane is the shearing force on this plane. Tensile stress= force/area =F cos θ/A sec θ =(F/A)cos2θ
(∵ Area of cross-section = Asecθ )
(b)Shearing stress= force/Area = Fsinθ/Asecθ=(F/2A)sin2θ
(c ) Obviously , tensile stress on the plane is maximum when cos2θ is maximum that is cos θ=1
or θ=0∘
(d) Obviously , shearing stress is maximum when sin 2θ is maximum ,
i.e. sin 2θ=1
or 2θ=90∘⇒θ=45∘
Topper's Solved these Questions
- ELASTICITY AND WAVES BOOK - FIITJEECHAPTER - ELASTICITY AND WAVES EXERCISE - Solved Problems
27 Videos
- ELASTICITY AND WAVES BOOK - FIITJEECHAPTER - ELASTICITY AND WAVES EXERCISE - Comprehension
16 Videos
- CURRENT ELECTRICITYBOOK - FIITJEECHAPTER - CURRENT ELECTRICITYEXERCISE - Comprehension -4
3 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - FIITJEECHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - EXERCISE
9 Videos
Similar Questions
A bar of cross-section A is subjected to equal and opposite tensile forces at its ends. Consider a plane section of the bar whose normal makes an angle θ with the axis of the bar .
(i) What is the tensile stress on this plane?
(ii) What is the shearing stress on this plane?
(iii) For what value of θ is the tensile stress maximum
(iv) For what value of θ is the shearing stress maximum?
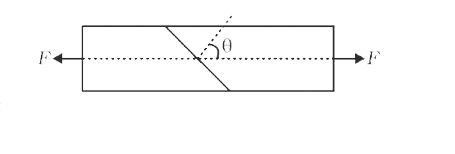
View SolutionA bar of cross section A is subjected to equal and opposite tensile force at its ends. Consider a plane section of the bar whose normal makes an angle θ with the axis of the bar.

a. What is the tensile stress on the plane?
b. What is the shearing stress on the this plane?
c. For what value of θ is the tensile stress maximum?
d. For what value of θ is the shearing stress maximum?
View Solution
Knowledge Check
A bar of cross- sectional area A is is subjected two equal and opposite tensile forces at its ends as shown in figure. Consider a plane BB' making an angle θ with length
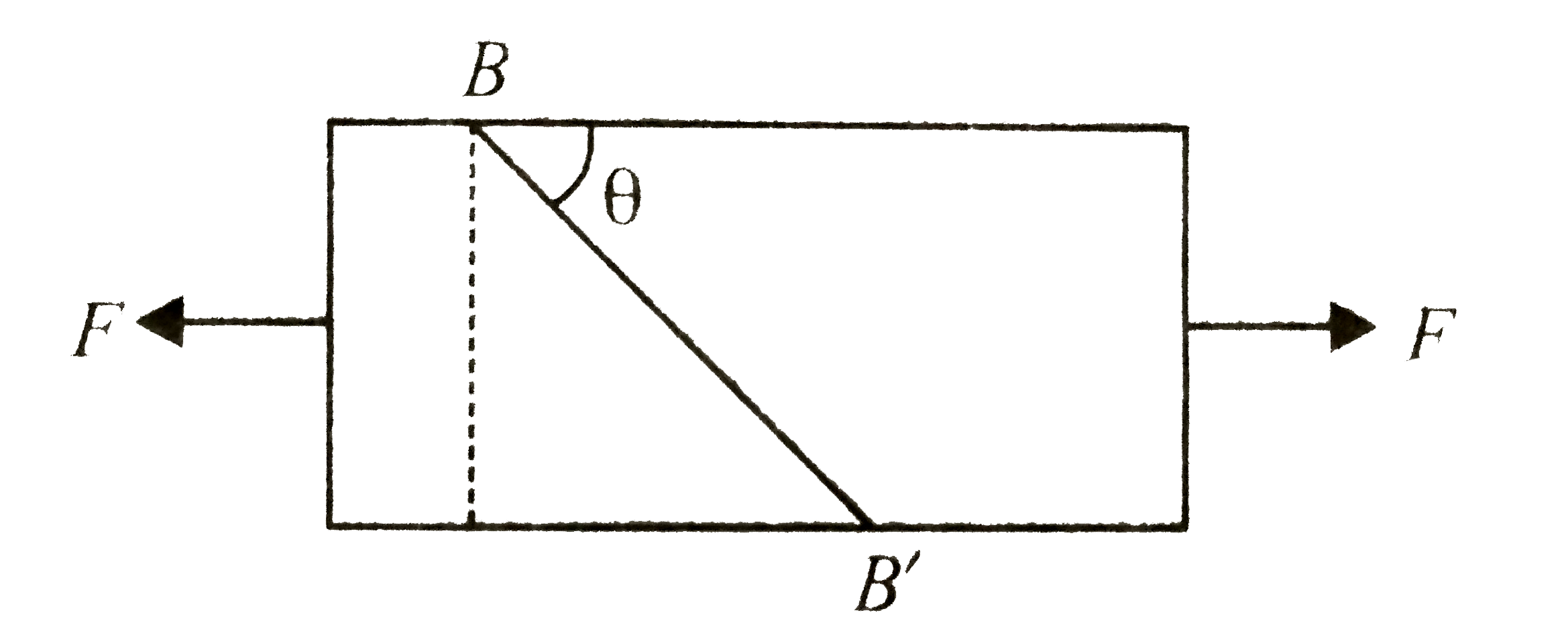 AtanθBsecθCcotθDcosθ
AtanθBsecθCcotθDcosθIn the question rumber 66, for what value of θ, shearing stress is maximum?
A0∘B30∘C45∘D90∘In the above problem, for what angle is the shearing stress a maximum?
A30∘B45∘C60∘D90∘
A bar of cross section A is subjected to equal and opposite tensile forces F at its ends. Consider a plane through the bar making an angle θ with a plane at right angles to the bar as shown in figure.
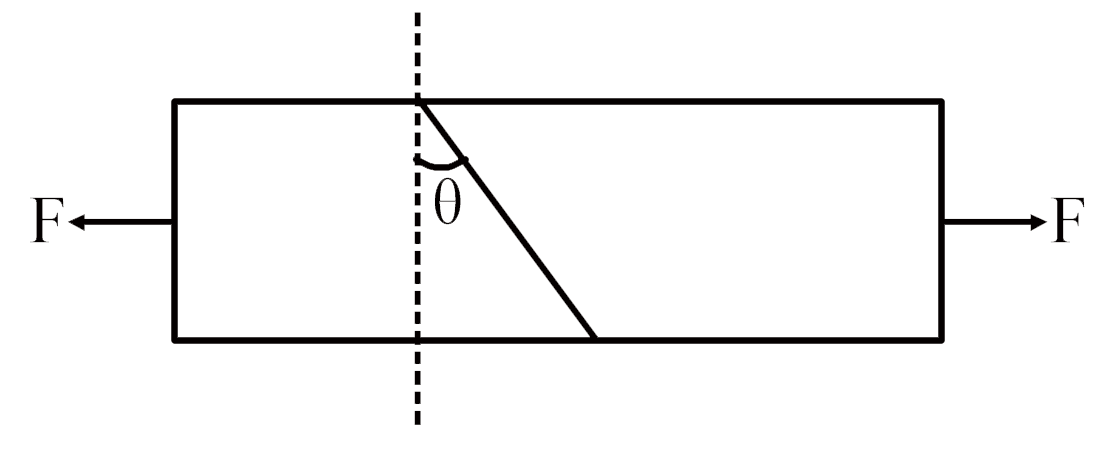
The tensile stress at this plane in terms of F, A and θ is
View SolutionA bar of cross section A is subjected to equal and opposite tensile forces F at its ends. Consider a plane through the bar making an angle θ with a plane at right angles to the bar as shown in figure.
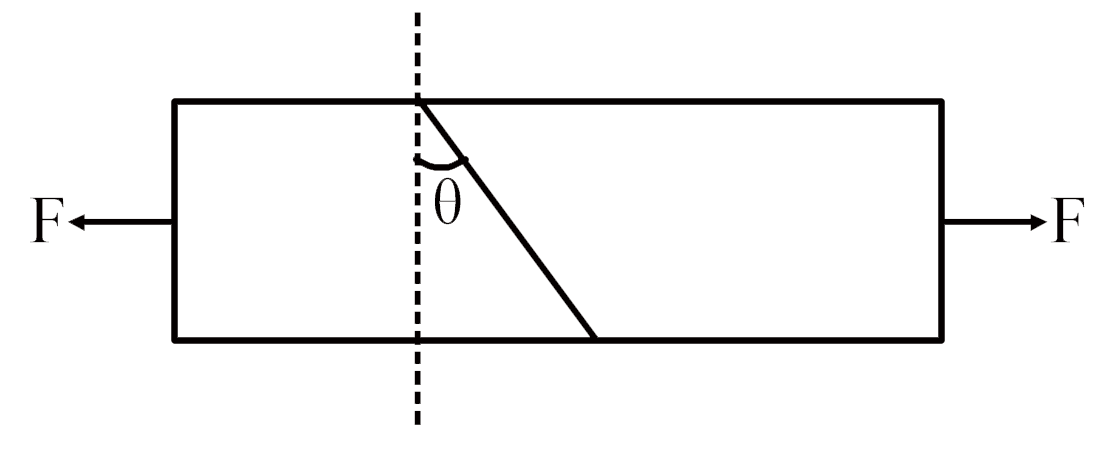
The shearing stress at the plane, in terms of F, A and θ is
View SolutionA bar of cross section A is subjected to equal and opposite tensile forces F at its ends. Consider a plane through the bar making an angle θ with a plane at right angles to the bar as shown in figure.

In the above problem, for what value of θ is the tensile stress maximum ?
View SolutionA steel bar of cross section A is subjected to two equal and opposite pulling forces at the two ends. If there is a plane through the bar making an angle α as shown, find

the shearing stress at this plane
View SolutionA steel bar of cross section A is subjected to two equal and opposite pulling forces at the two ends. If there is a plane through the bar making an angle α as shown, find

for what α the shearing strain is maximum.
View Solution
