Two uniform circular discs having the same mass and the same thickness but different radii are made from different materials. The disc with the smaller rotational inertia isSolution in Telugu
The one made from the more dense material
The one made from the less dense material
The disc with the larger angular velocity
The disc with the larger torque
The correct Answer is:(b)
The expression for moment of inertia of circular disc is given as,
I=12MR2
=12M(Mπtp) (∵M=πR2tp⇒R2=Mπtp)
12M2πtp When the thickness and mass becomes equal, we get,
I=∝1p When the disc with the smaller rotational inertia is the one made from the denser material.
Topper's Solved these Questions
Similar Questions
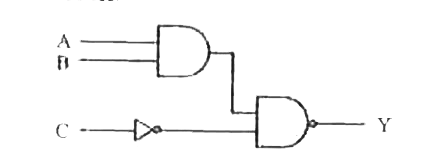
In the following circuit the output Y becomes zero for the input combinations
View SolutionThe specific heat of helium at constant volume is 12.6Jmol−1K−1. The specific heat of helium at constant pressure in Jmol−1K−1 is about
(Assume the temperature of the gas is moderate, universal gas constant, R=8.314Jmol−1K−1
View SolutionTwo discs of the same material and thickness have radii 0.2 m and 0.6 m. Their moments of inertia about their axes will be in the ratio of
View SolutionTwo discs of same thickness but of different radii are made of two different materials such that their masses are same. The densities of the materials are in the ratio of 1 : 3. The moments of inertia of these discs about the respective axes passing through their centres and perpendicular to their planes will be in the ratio of
View SolutionIf two circular discs A and B are of same mass but of radii r and 2r respectively, then the moment of inertia of A is
View SolutionThe angular momentum of two circular discs is same. The mass of the first disc is more than second disc then the rotational K.E. is more for
View SolutionAssertion (A) Two circular discs of equal mass and thickness made of different materials, will have same moment of inertia about their central axes of rotation.
Reason (R) Moment of inertia depends upon the distribution of mass in the body.
View SolutionTwo discs of same material have the same mass. If their thickness are in the ratio 1:3, then their moment of inertia are in the ratio
View SolutionTwo discs of same material have the same mass. If their thickness are in the ratio 1:3 , then their moment of inertia are in the ratio
View SolutionTo discs have same moment of inertia about their own axes . Their thickness are also same . If the ratio of their material densities is 16 :1 . Find the ratio of their radii .
View Solution(A) : Two circular discs of equal masses and thickness made of different material, will have same moment of inertia about their central axes of rotation.
(R ) : Moment of inertia depends upon the distribution of mass in the body.
View SolutionThree circular discs of same material and same thickness of radii r, 2r and 3r are placed on a horizontal plane such that their centres lie along a straight line. The radius of the middle disc is 2r and it touches the other two discs. The distance of the centre of mass of the system from the centre of the smaller disc is
View SolutionTwo discs of same thickness but of different radii are made of two different materials such that their masses are same. The densities of the materials are in the ratio of 1:3. The moments of inertia of these discs about the respective axes passing through their centres and perpendicular to their planes will be in the ratio of
View SolutionTwo discs A and B have same mass and same thickness. If d1 and d2 are the densities of the materials of the discs A and B respectively, then the ratio of the moment of inertia of the discs A and B about their geometrical axis is
View SolutionIf two circular discs A and B are of same mass but of radii r and 2r respectively, then the moment of inertia of A is
View Solution

