Assume the earth's orbit around the sun as circular and the distance between their centres as D. Mass of the earth is M and its radius is R. If earth has an angular velocity with respect to its centre and with respect to the centre of the sun, the total kinetic energy of earth isSolution in Telugu
MR25ω20[1+(ωω0)2+52(DωRω0)2]
MR25ω20[1+52(DωRω0)2]
23MR2ω20[1+52(DωRω0)2]
25MR2ω20[1+(ωω0)2+52(DωRω0)2]
The correct Answer is:(b)
Kinetic energy of earth with respect to its centre is,
KE1=12Iω20
=12×25MR2×ω20
Kinetic energy of earth with respect to the sun is,
KE1=12Iω20
12×MR2(D2R2)ω2
Total kinetic energy K.ETotal
KE1+KE2
=12×25MR2×ω20+12×MR2(D2R2)ω2
MR2ω205[1+52(Dω(Rω0)2)]

Topper's Solved these Questions
Similar Questions
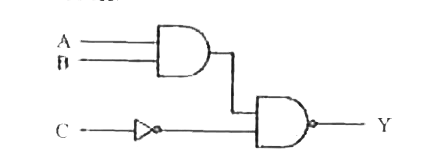
In the following circuit the output Y becomes zero for the input combinations
View SolutionThe specific heat of helium at constant volume is 12.6Jmol−1K−1. The specific heat of helium at constant pressure in Jmol−1K−1 is about
(Assume the temperature of the gas is moderate, universal gas constant, R=8.314Jmol−1K−1
View SolutionA satellite of mass m is in a circular orbit of radius r round the Earth. Calculate its angular momentum with respect to the centre of the orbit in terms of the mass M of the Earth and G .
View SolutionAssume the earth's orbit around the sun as circular and the distance between their centres as D Mass of the earth is M and its radius is R if earth has an angular velocity omega_0 with respect to its centre and omega with respect to the centre of the sun, the total kinetic energy of the earth is:
View SolutionA satellite of mass m is revolving around the earth at a distancer r from the centre of the earth. What is its total energ?
View SolutionIf mass density of earth varies with distance 'r' from centre of earth as ρ=krand'R'isradius of earth, then find the orbital velocity of an object revolving around earth at adistance '2R' from its centre.
View Solutionr denotes the distance between the sun and the earth. Assume that the earth moves around the sun in a circular orbit of radius r. The angular momentum of the earth around the sun is proportional to
View SolutionA satellite of mass m revolves around the earth in a circular orbit of radius r. Find the angular momentum of the satellite with respect to the centre of the orbit.
View SolutionAssuming that the earth revolves around the sun in a circular orbit, the line joining the earth and the centre of its orbit covers………area. [Fill in the blanks]
View SolutionA satellite of mass m is circulating around the earth with constant angular velocity. If radius of the orbit is r and mass of the earth M, the angular momentum about the centre of the earth is :
View SolutionAn artificial,satellite of mass .m. is revolving around the earth, in a circular orbit of radius .r.. If the mass of the earth is.m. angular momentum of the satellite with respect to the centre of earth is (G-universal gravitational constant):
View SolutionAn artificial satellite of mass 'm' is revolving around the earth, in a circular orbit of radius 'r'. If the mass of the earth is 'm' angular momentum of the satellite with respect to the centre of earth is (G-universal gravitational constant)
View SolutionAn artificial satellite of mass 'm' is revolving around the earth, in a circular orbit of radius 'r'. If the mass of the earth is 'm' angular momentum of the satellite with respect to the centre of earth is (G= universal gravitational constant)
View SolutionAn artificial satellite of mass 'm' is revolving around the earth, in a circular orbit of radius 'r'. If the mass of the earth is 'm' angular momentum of the satellite with respect to the centre of earth is (G-universal gravitational constant)
View SolutionAn artificial satellite of mass 'm' is revolving around the earth, in a circular orbit of radius 'r'. If the mass of the earth is 'm' angular momentum of the satellite with respect to the centre of earth is (G= universal gravitational constant)
View Solution
