The instantaneous velocity of a particle moving in a straight line is given as a function of time by: v=v0(1−(tt0)n) where t0 is a constant and n is a positive integer . The average velocity of the particle between t=0 and t=t0 is 3v04.Then , the value of n is
The correct Answer is:C
To solve the problem, we need to find the value of n given the instantaneous velocity function and the average velocity over a specified time interval. Let's break down the solution step by step.
Step 1: Write down the given instantaneous velocity function
The instantaneous velocity of the particle is given by:
v=v0(1−(tt0)n)
Step 2: Relate velocity to displacement
We know that:
v=dxdt
Thus, we can express dx in terms of dt:
dx=v0(1−(tt0)n)dt
Step 3: Integrate to find displacement
We need to find the displacement x from t=0 to t=t0:
x=∫t00v0(1−(tt0)n)dt
This can be split into two parts:
x=v0∫t00dt−v0∫t00(tt0)ndt
Step 4: Calculate the first integral
The first integral is straightforward:
∫t00dt=t0
Thus, the first part becomes:
v0⋅t0
Step 5: Calculate the second integral
For the second integral:
∫t00(tt0)ndt=1tn+10∫t00tndt
Using the formula for the integral:
∫tndt=tn+1n+1
we get:
∫t00tndt=tn+10n+1
Thus, the second part becomes:
1tn+10⋅tn+10n+1=t0n+1
Step 6: Combine the results for displacement
Now, substituting back into the expression for x:
x=v0t0−v0⋅t0n+1=v0t0(1−1n+1)=v0t0⋅nn+1
Step 7: Calculate the average velocity
The average velocity ¯v over the interval t=0 to t=t0 is given by:
¯v=ΔxΔt=xt0
Substituting for x:
¯v=v0t0⋅nn+1t0=v0⋅nn+1
Step 8: Set the average velocity equal to the given value
We are given that the average velocity is 3v04:
v0⋅nn+1=3v04
Dividing both sides by v0 (assuming v0≠0):
nn+1=34
Step 9: Solve for n
Cross-multiplying gives:
4n=3(n+1)
Expanding and simplifying:
4n=3n+3⟹n=3
Final Answer
The value of n is:
3
The instantaneous velocity of the particle is given by:
v=v0(1−(tt0)n)
We know that:
v=dxdt
Thus, we can express dx in terms of dt:
dx=v0(1−(tt0)n)dt
We need to find the displacement x from t=0 to t=t0:
x=∫t00v0(1−(tt0)n)dt
This can be split into two parts:
x=v0∫t00dt−v0∫t00(tt0)ndt
The first integral is straightforward:
∫t00dt=t0
Thus, the first part becomes:
v0⋅t0
For the second integral:
∫t00(tt0)ndt=1tn+10∫t00tndt
Using the formula for the integral:
∫tndt=tn+1n+1
we get:
∫t00tndt=tn+10n+1
Thus, the second part becomes:
1tn+10⋅tn+10n+1=t0n+1
Now, substituting back into the expression for x:
x=v0t0−v0⋅t0n+1=v0t0(1−1n+1)=v0t0⋅nn+1
The average velocity ¯v over the interval t=0 to t=t0 is given by:
¯v=ΔxΔt=xt0
Substituting for x:
¯v=v0t0⋅nn+1t0=v0⋅nn+1
We are given that the average velocity is 3v04:
v0⋅nn+1=3v04
Dividing both sides by v0 (assuming v0≠0):
nn+1=34
Cross-multiplying gives:
4n=3(n+1)
Expanding and simplifying:
4n=3n+3⟹n=3
The value of n is:
3
Similar Questions
The instantaneous velocity of a particle moving in a straight line is given as v=αt+βt2, where α and β are constants. The distance travelled by the particle between 1s and 2s is :
View SolutionThe velocity of a particle moving along the xaxis is given by v=v0+λx, where v0 and lambda are constant. Find the velocity in terms of t.
View Solution
Knowledge Check
The velocity of an object moving rectillinearly is given as a functiion of time by v=4t−3t2 where v is in m/s and t is in seconds. The average velociy if particle between t=0 to t=2 seconds is
A0B−2m/sC−4m/sD+2m/sThe velocity 'v' of a particle moving along straight line is given in terms of time t as v=3(t2−t) where t is in seconds and v is in m/s.
The speed is minimum after t=0 second at instant of timeA0.5secB1secC2secDNone of theseThe velocity 'v' of a particle moving along straight line is given in terms of time t as v=3(t2−t) where t is in seconds and v is in m/s.
The distance travelled by particle from t=0 to t=2seconds is :A2mB3mC4mD6m
A particle moving along x axis has acceleration f at time t given by f=f0(1−1t) where f0 and T are constant the particle at T=0 has zero velocity in the time interval between t=0 and the instant when f=0 the particle velocity vx is
View SolutionThe velocity 'v' of a particle moving along straight line is given in terms of time t as v=3(t2−t) where t is in seconds and v is in m/s.
The displacement of aprticle from t=0 to t=2 seconds is :
View SolutionA particle moving along x-axis has acceleration f, at time t, given by f=f0(1−tT), where f0 and T are constants. The particle at t= 0 has zero velocity. In the time interval between t= 0 and the instant when f= 0, the particle's velocity (vx) is
View SolutionA particle moving along x-axis has acceleration f, at time t, given by f=f0(1−tT), where f0 and T are constant.
The particle at t=0 has zero velocity. In the time interval between t=0 and the instant when f=0, the particle's velocity (vx) is :
View SolutionAcceleration time graph of a particle moving along a straight line is given. Then average acceleration between t=0 & t=4 is :−
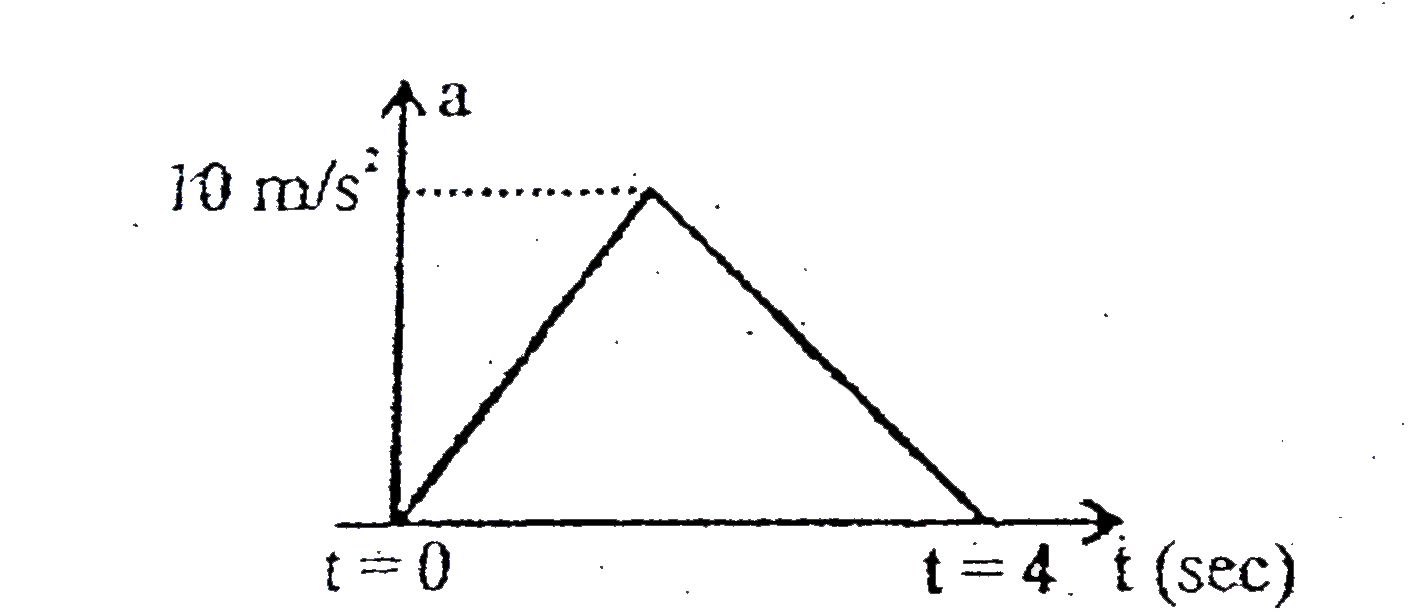
View Solution
