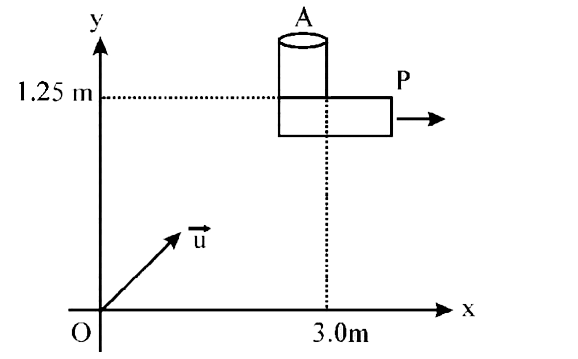
An object A is kept fixed at the point x=3m and y=1.25m on a plank p raised above the ground . At time t=0 the plank starts moving along the +x direction with an acceleration 1.5m/s2. At the same instant a stone is projected from the origin with a velocity →u as shown . A stationary person on the ground observes the stone hitting the object during its downward motion at an angle 45(∘) to the horizontal . All the motions are in the X−Yplane . Find →u and the time after which the stone hits the object . Take g=10m/s
The correct Answer is:1s
Let after time ‘t’ the stone hits the object and be the angle which the velocity vector makes with horizontal
From question, we have following information Vertical displacement of stone is 1.25 m
Using sy=uyt+12ayt2
Therefore 1.25 =(usinθ)t−12>2or(usinθ)t=1.25+5t2...(i)
Horizontal displacement of stone = 3 + displacement of object A.
Therefore (ucosθ)t=3+12at2
We have a=1.5m/s2,Hence (ucosθ)t=3+0.75t2.....(ii)
Horizontal component of velocity (of stone) = vertical component (because velocity vector is inclined at 45∘ with horizontal).
Therefore (ucosθ)=>−(usinθ)........(iii)
The right-hand side is written because the stone is in its downward motion. Therefore >>usinθ
Multiplying equation (iii) with t can write. (ucosθ)t+(usinθ)t=10t2......(iv)
Now doing (iv)-[(iii)+(i)]
It gives 4.25t2−4.25ort=1s Substituting t=1 s in (i) and (ii) we get
usinθ=6.25m/sorvy=6.25manducosθ=3.75m/sorux=3.75m/s
Now, we can write u=uxˆi+uyˆioru=(3.75ˆi+6.25ˆj)m/s 
Similar Questions
Acceleration of a particle in x-y plane varies with time as a=(2tˆi+3t2ˆj)m/s2 At time t=0, velocity of particle is 2m/s along positive x direction and particle starts from origin. Find velocity and coordinates of particle at t=1s.
View SolutionA man of mass m is moving with a constant acceleration a w.r.t plank is .The plank less on a smooth horizontal floor If the mass of plank m then calculate the acceleration of plank and man w.r.t ground and frictional force extended by plank on man
View SolutionA stone is projected from level ground at t=0 sec such that its horizontal and vertical components of initial velocity are 10(m)/(s) and 20(m)/(s) respectively. Then the instant of time at which tangential and normal components of acceleration of stone are same is: (neglect air resistance) g=10(m)/(s^2) .
View SolutionA man of mass m moves on a plank of mass M with a constant velocity u with respect to the plank, as shown in figure. a.If the plank rests on smooth horizontal surface, determine the velocity of the plank. .
View SolutionA man of mass m starts moving on a plank of mass M with constant velocity v with respect to plank. If the plank lies on a smooth horizontal surface, then velocity of plank with respect to ground is
View SolutionA stone is projected from level ground at t=0 sec such that its horizontal and vertical components of initial velocity are 10(m)/(s) and 20(m)/(s) respectively. Then the instant of time at which tangential and normal components of acceleration of stone are same is: (neglect air resistance) g=10(m)/(s^2) .
View SolutionAn object A is kept fixed at the point x=3m and y=1.25m on a plank p raised above the ground . At time t=0 the plank starts moving along the +x direction with an acceleration 1.5m/s2. At the same instant a stone is projected from the origin with a velocity →u as shown . A stationary person on the ground observes the stone hitting the object during its downward motion at an angle 45(∘) to the horizontal . All the motions are in the X−Yplane . Find →u and the time after which the stone hits the object . Take g=10m/s

View SolutionA particle starts from the origin at t = 0 s with a velocity of 10.0ˆjm/s and moves in the x-y plane with a constant acceleration of (8.0ˆi+2.0ˆj)ms−2,:- What is the speed of the particle at the time ?
View Solution
