Speed of a planet in an ellioptical orbit with semimajor axis a about sun of mass M at a distance r from sun is
√GM(2r−1a)
√GM(1r−1a)
√GM(1r−2a)
√GMr2a2
The correct Answer is:A
Step by step video, text & image solution for Speed of a planet in an ellioptical orbit with semimajor axis a about sun of mass M at a distance r from sun is by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
A planet of mass m revolves in elliptical orbit around the sun of mass M so that its maximum and minimum distance from the sun equal to ra and rp respectively. Find the angular momentum of this planet relative to the sun.
View SolutionIf a planet revolve around the sun in an elliptical orbit such that its minimum distance from sun is r1 and maximum distance is r2. Find the distance of planet from sun when it is at a position where the line joining the planet and sun is perpendicular to the major axis of ellipse.
View Solution
Knowledge Check
A planet moves around the sun in an elliptical orbit. When earth is closest from the sun, it is at a distance r having a speed v. When it is at a distance 4r from the sun its speed will be:
A4vBv4C2vDv2A planet is revolving around the Sun in an elliptical orbit. Its closest distance from the sun is rmin. The farthest distance from the sun is rmax if the orbital angular velocity of the planet when it is nearest to the Sun ω then the orbital angular velocity at the point when it i at the farthest distanec from the sun is
A(√rminrmax)ωB(√rmaxrmin)ωC(rmaxrmin)2ωD(rminrmax)2ωA planet is revolving in an elliptical orbit around the sun. Its closest distance from the sun is r and the farthest distance is R. If the velocity of the planet nearest to the sun be v and that farthest away from the sun be V. then v/V is
AR2/r2Br2/R2CR/rDr/R
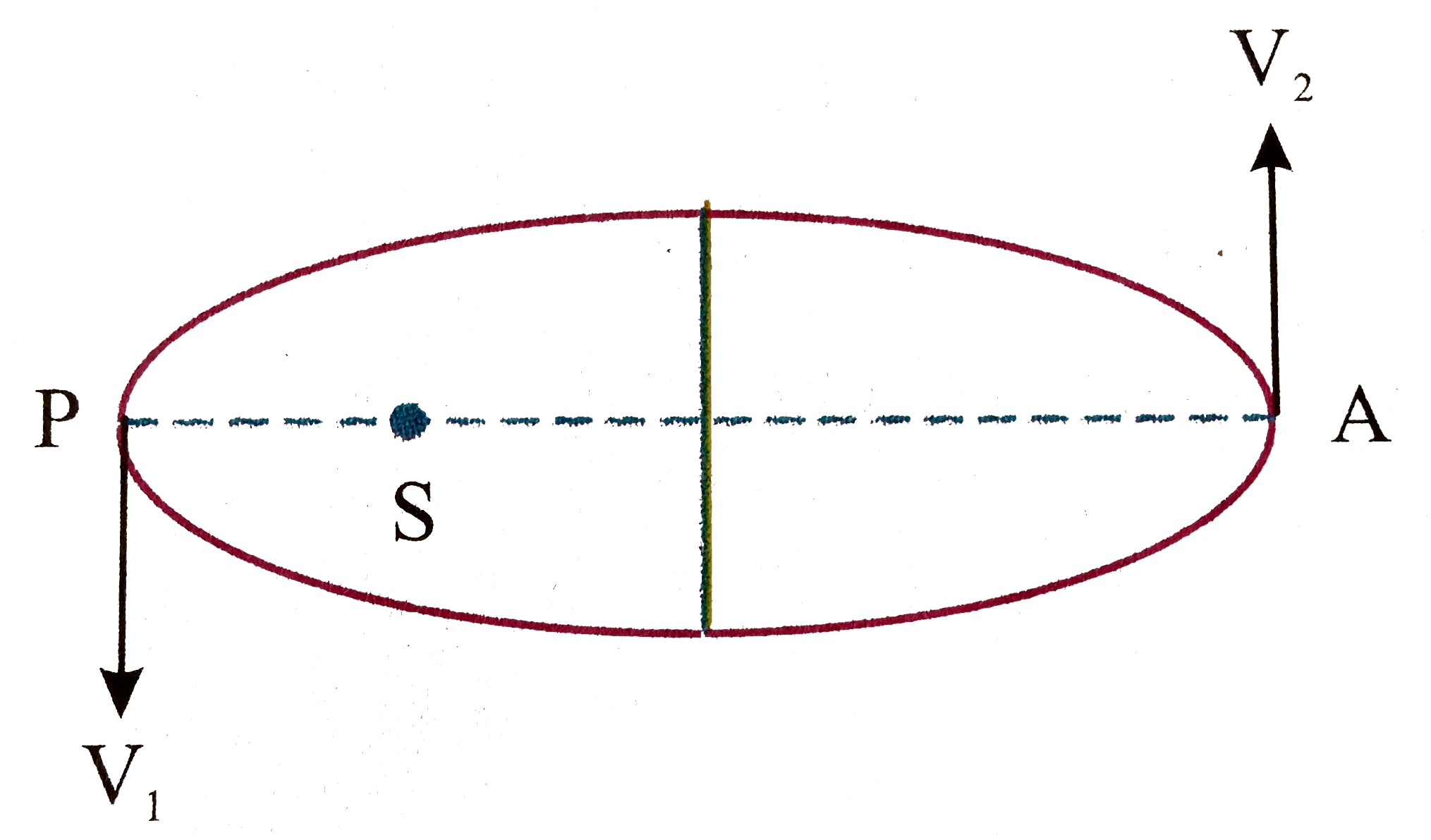
A planet of mass m is moving in an elliptical orbit around the sun of mass M. The semi major axis of its orbit is a, eccentricity is e.
Find speed of planet V2 at aphelion A.
View Solution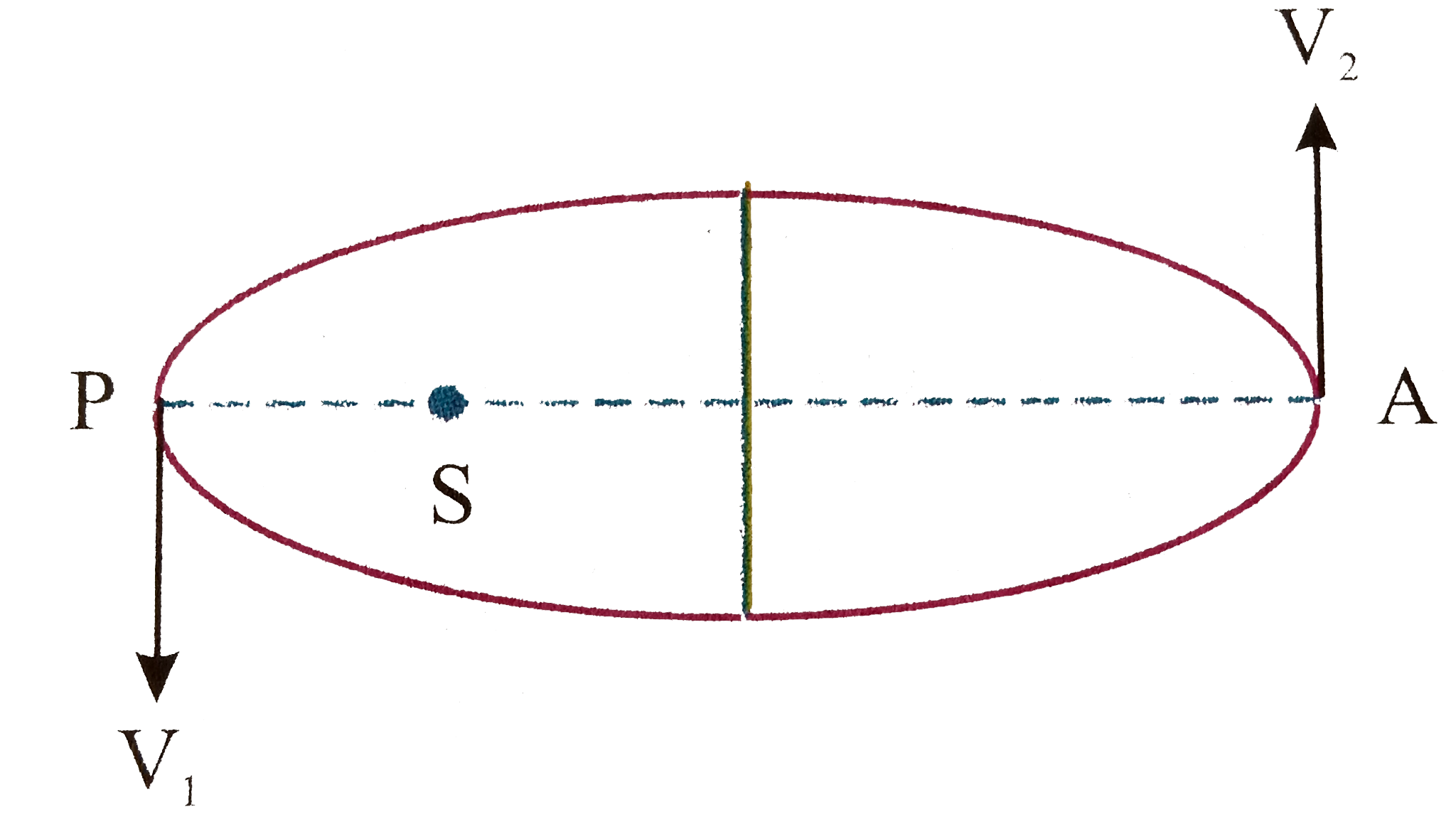
A planet of mass m is moving in an elliptical orbit around the sun of mass M. The semi major axis of its orbit is a, eccentricity is e.
Find speed of planet V1 at perihelion P
View Solution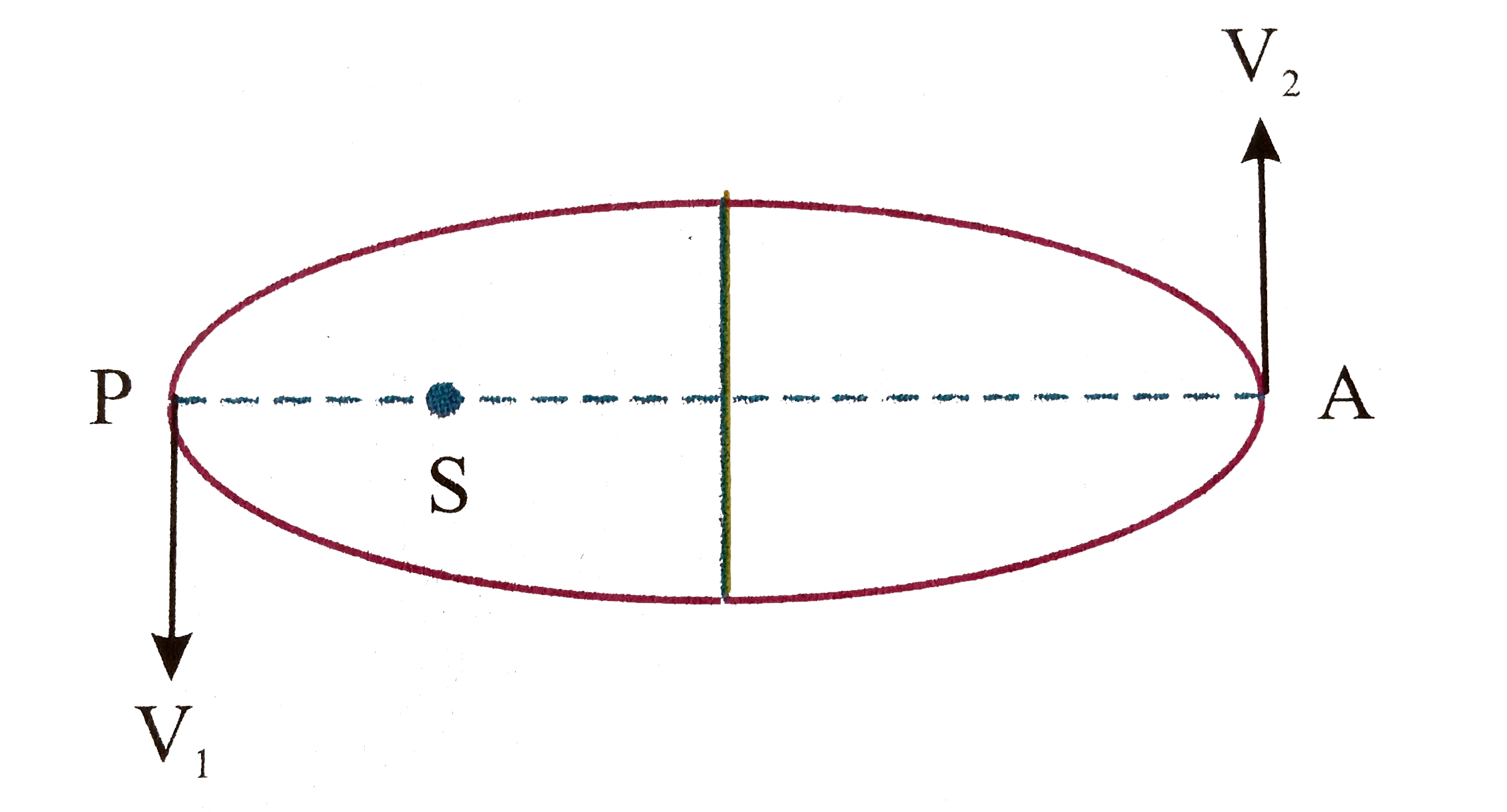
A planet of mass m is moving in an elliptical orbit around the sun of mass M. The semi major axis of its orbit is a, eccentricity is e.
Find total energy of planet interms of given parameters.
View SolutionA planet is revolving around the Sun in an elliptical orbit. Its closest distance from the Sun is r and farthest distance is R. If the orbital velocity of the planet closest to the Sun is v, then what is the velocity at the farthest point?
View SolutionA planet of small mass m moves around the sun of mass M along an elliptrical orbit such that its minimum and maximum distance from sun are r and R respectively. Its period of revolution will be:
View Solution

