Question

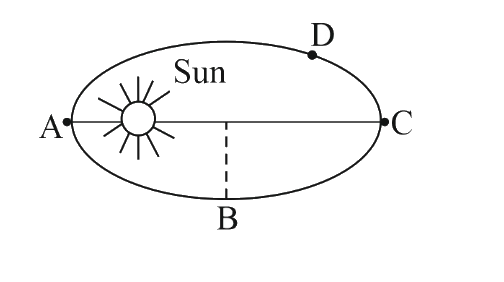
A planet is revolving around the Sun in an elliptical orbit. Its closest distance from the Sun is $r$ and farthest distance is $R$. If the orbital velocity of the planet closest to the Sun is $v$, then what is the velocity at the farthest point?

Options

A. `(vr)/R`
B. `(vR)/r`
C. `vsqrt(r/R)`
D. `vsqrt(R/r)`

Answer

A

Explanation

To find the velocity of the planet at its farthest point from the Sun in its elliptical orbit, we can use the principle of conservation of angular momentum. Here’s a step-by-step solution:

Step 1: Understand the problem
We have a planet revolving around the Sun in an elliptical orbit. The closest distance from the Sun is denoted as `r`, and the farthest distance is `R`. The velocity of the planet at the closest point is `v`, and we need to find the velocity at the farthest point, which we will denote as `V`.

Step 2: Use the conservation of angular momentum
In an elliptical orbit, the angular momentum of the planet remains constant. The angular momentum (L) at any point in the orbit can be expressed as:
\( L = m \cdot v \cdot r \)
at the closest point, and
\( L = m \cdot V \cdot R \)
at the farthest point, where:
- \( m \) is the mass of the planet,
- \( v \) is the velocity at the closest point,
- \( r \) is the distance from the Sun at the closest point,
- \( V \) is the velocity at the farthest point,
- \( R \) is the distance from the Sun at the farthest point.

Step 3: Set the angular momentum equations equal
Since angular momentum is conserved, we can set the two expressions for angular momentum equal to each other:
\( m \cdot v \cdot r = m \cdot V \cdot R \)

Step 4: Simplify the equation
We can cancel the mass \( m \) from both sides of the equation:
\( v \cdot r = V \cdot R \)

Step 5: Solve for the velocity at the farthest point
Now, we can solve for \( V \):
\( V = \frac{v \cdot r}{R} \)

Final Result
Thus, the velocity of the planet at the farthest point from the Sun is:
\( V = \frac{v \cdot r}{R} \)

---