The graph between the angular momentum J and angular velocity ω will be :-
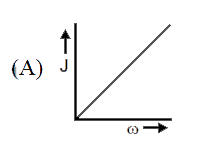

The correct Answer is:A
To find the relationship between angular momentum J and angular velocity ω, we can follow these steps:
Step 1: Understand the Formula for Angular Momentum
The angular momentum J of a rotating object is given by the formula:
J=I⋅ω
where I is the moment of inertia and ω is the angular velocity.
Step 2: Identify the Variables
In this equation:
- J (angular momentum) is the dependent variable.
- ω (angular velocity) is the independent variable.
- I (moment of inertia) is a constant for a given object.
Step 3: Rearranging the Equation
The equation can be rearranged to express J in terms of ω:
J=I⋅ω
This indicates that J is directly proportional to ω.
Step 4: Graphing the Relationship
To graph this relationship:
- Let J be on the y-axis and ω be on the x-axis.
- The equation J=I⋅ω is in the form of y=mx, where:
- y is J,
- x is ω,
- m (the slope) is I, and
- there is no y-intercept (c = 0).
Step 5: Conclusion about the Graph
Since the graph passes through the origin (0,0) and has a slope equal to the moment of inertia I, the graph between angular momentum J and angular velocity ω will be a straight line through the origin.
Final Answer
The graph between angular momentum J and angular velocity ω is a straight line passing through the origin.
---
The angular momentum J of a rotating object is given by the formula:
J=I⋅ω
where I is the moment of inertia and ω is the angular velocity.
In this equation:
- J (angular momentum) is the dependent variable.
- ω (angular velocity) is the independent variable.
- I (moment of inertia) is a constant for a given object.
The equation can be rearranged to express J in terms of ω:
J=I⋅ω
This indicates that J is directly proportional to ω.
To graph this relationship:
- Let J be on the y-axis and ω be on the x-axis.
- The equation J=I⋅ω is in the form of y=mx, where:
- y is J,
- x is ω,
- m (the slope) is I, and
- there is no y-intercept (c = 0).
Since the graph passes through the origin (0,0) and has a slope equal to the moment of inertia I, the graph between angular momentum J and angular velocity ω will be a straight line through the origin.
The graph between angular momentum J and angular velocity ω is a straight line passing through the origin.
Topper's Solved these Questions
- ROTATIONAL MOTION Book:MOTIONChapter:ROTATIONAL MOTION Exercise:Exercise - 2
Explore 40 Videos
- ROTATIONAL MOTION Book:MOTIONChapter:ROTATIONAL MOTION Exercise:Exercise - 3 ( Section-A )
Explore 46 Videos
- ROTATIONAL MOTION Book:MOTIONChapter:ROTATIONAL MOTION Exercise:Exercise - 3 ( Section-B )
Explore 24 Videos
- RAY OPTICSBook:MOTIONChapter:RAY OPTICSExercise:Exercise-4
Explore 38 Videos
- SEMI CONDUCTOR AND LOGIC GATESBook:MOTIONChapter:SEMI CONDUCTOR AND LOGIC GATESExercise:EXERCISE 3
Explore 34 Videos
Similar Questions
Knowledge Check
Angular momentum is
Amoment of momentumBproduct of mass and angular velocityCproduct of moment of inertia and velocityDmoment in angular motionAngular momentum is
Amoment of momentumBproduct of mass and angular velocityCproduct of moment of inertia and velocityDmoment in angular motionAngular momentum is
Amoment of momentumBproduct of mass and angular velocityCproduct of moment of inertia and velocityDmoment in angular motion
Angular momentum||Examples on angular momentum
View SolutionThe angular momentum is?
View SolutionThe graph between wave number (→v) and angular frequency (ω) is
View SolutionRelation between Linear velocity (v) and Angular velocity (ω)
View SolutionA swing moving in a children's garden is observed to move with an angular velocity given by, ω−a(t2)ˆi+b(e−1)ˆj. What will be the angle between angular acceleration and angular velocity at t=1 s given that a=b=1 unit?
View Solution